

2000年全国硕士研究生入学统一考试
数学(一)试卷
一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)
(1)![]() =_____________.
=_____________.
(2)曲面![]() 在点
在点![]() 的法线方程为_____________.
的法线方程为_____________.
(3)微分方程![]() 的通解为_____________.
的通解为_____________.
(4)已知方程组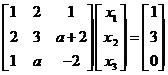 无解,则
无解,则![]() = _____________.
= _____________.
(5)设两个相互独立的事件![]() 和
和![]() 都不发生的概率为
都不发生的概率为![]() ,
,![]() 发生
发生![]() 不发生的概率与
不发生的概率与![]() 发生
发生![]() 不发生的概率相等,则
不发生的概率相等,则![]() =_____________.
=_____________.
二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)
(1)设![]() 、
、![]() 是恒大于零的可导函数,且
是恒大于零的可导函数,且![]() ,则当
,则当![]() 时,有
时,有
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(2)设![]() 为
为![]() 在第一卦限中的部分,则有
在第一卦限中的部分,则有
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(3)设级数![]() 收敛,则必收敛的级数为
收敛,则必收敛的级数为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(4)设![]() 维列向量组
维列向量组![]() 线性无关,则
线性无关,则![]() 维列向量组
维列向量组![]() 线性无关的充分必要条件为
线性无关的充分必要条件为
(A)向量组![]() 可由向量组
可由向量组![]() 线性表示
线性表示
(B)向量组![]() 可由向量组
可由向量组![]() 线性表示
线性表示
(C)向量组![]() 与向量组
与向量组![]() 等价
等价
(D)矩阵![]() 与矩阵
与矩阵![]() 等价
等价
(5)设二维随机变量![]() 服从二维正态分布,则随机变量
服从二维正态分布,则随机变量![]() 与
与 ![]() 不相关的充分必要条件为
不相关的充分必要条件为
(A)![]() (B)
(B)![]()
![]()
(C)![]() (D)
(D)![]()
三、(本题满分6分)
求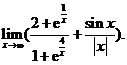
四、(本题满分5分)
设![]() ,其中
,其中![]() 具有二阶连续偏导数
具有二阶连续偏导数![]() 具有二阶连续导数,求
具有二阶连续导数,求![]()
五、(本题满分6分)
计算曲线积分![]() ,其中
,其中![]() 是以点
是以点![]() 为中心
为中心![]() 为半径的圆周
为半径的圆周![]() 取逆时针方向.
取逆时针方向.
六、(本题满分7分)
设对于半空间![]() 内任意的光滑有向封闭曲面
内任意的光滑有向封闭曲面![]() 都有
都有![]() 其中函数
其中函数![]() 在
在![]() 内具有连续的一阶导数,且
内具有连续的一阶导数,且![]() 求
求![]() .
.
七、(本题满分6分)
求幂级数![]() 的收敛区间,并讨论该区间端点处的收敛性.
的收敛区间,并讨论该区间端点处的收敛性.
八、(本题满分7分)
设有一半径为![]() 的球体
的球体![]() 是此球的表面上的一个定点,球体上任一点的密度与该点到
是此球的表面上的一个定点,球体上任一点的密度与该点到![]() 距离的平方成正比(比例常数
距离的平方成正比(比例常数![]() ),求球体的重心位置.
),求球体的重心位置.
九、(本题满分6分)
设函数![]() 在
在![]() 上连续,且
上连续,且![]() 试证:在
试证:在![]() 内至少存在两个不同的点
内至少存在两个不同的点![]() 使
使![]()
十、(本题满分6分)
设矩阵![]() 的伴随矩阵
的伴随矩阵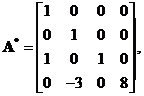 且
且![]() ,其中
,其中![]() 为4阶单位矩阵,求矩阵
为4阶单位矩阵,求矩阵![]() .
.
十一、(本题满分8分)
某适应性生产线每年1月份进行熟练工与非熟练工的人数统计,然后将![]() 熟练工支援其他生产部门,其缺额由招收新的非熟练工补齐.新、老非熟练工经过培训及实践至年终考核有
熟练工支援其他生产部门,其缺额由招收新的非熟练工补齐.新、老非熟练工经过培训及实践至年终考核有![]() 成为熟练工.设第
成为熟练工.设第![]() 年1月份统计的熟练工与非熟练工所占百分比分别为
年1月份统计的熟练工与非熟练工所占百分比分别为![]() 和
和![]() 记成向量
记成向量![]()
(1)求![]() 与
与![]() 的关系式并写成矩阵形式:
的关系式并写成矩阵形式: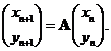
(2)验证![]() 是
是![]() 的两个线性无关的特征向量,并求出相应的特征值.
的两个线性无关的特征向量,并求出相应的特征值.
(3)当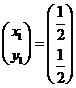 时,求
时,求![]()
十二、(本题满分8分)
某流水线上每个产品不合格的概率为![]() ,各产品合格与否相对独立,当出现1个不合格产品时即停机检修.设开机后第1次停机时已生产了的产品个数为
,各产品合格与否相对独立,当出现1个不合格产品时即停机检修.设开机后第1次停机时已生产了的产品个数为![]() ,求
,求![]() 的数学期望
的数学期望![]() 和方差
和方差![]() .
.
十三、(本题满分6分)
设某种元件的使用寿命![]() 的概率密度为
的概率密度为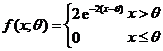 ,其中
,其中![]() 为未知参数.又设
为未知参数.又设![]() 是
是![]() 的一组样本观测值,求参数
的一组样本观测值,求参数![]() 的最大似然估计值.
的最大似然估计值.
2001年全国硕士研究生入学统一考试
数学(一)试卷
一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)
(1)设![]() 为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为_____________.
为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为_____________.
(2)![]() ,则
,则![]() = _____________.
= _____________.
(3)交换二次积分的积分次序:![]() =_____________.
=_____________.
(4)设![]() ,则
,则![]() = _____________.
= _____________.
(5)![]() ,则根据车贝晓夫不等式有估计
,则根据车贝晓夫不等式有估计![]() _____________.
_____________.
二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)
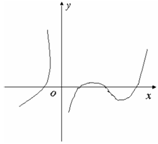
(1)设函数![]() 在定义域内可导,
在定义域内可导,![]() 的图形如右图所示,则
的图形如右图所示,则![]() 的图形为
的图形为
(A)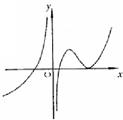 (B)
(B)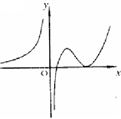
(C)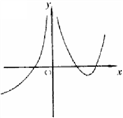 (D)
(D)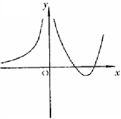
(2)设![]() 在点
在点![]() 的附近有定义,且
的附近有定义,且![]() 则
则
(A)![]()
(B)曲面![]() 在
在![]() 处的法向量为
处的法向量为![]()
(C)曲线 ![]() 在
在![]() 处的切向量为
处的切向量为![]()
(D)曲线 ![]() 在
在![]() 处的切向量为
处的切向量为![]()
(3)设![]() 则
则![]() 在
在![]() =0处可导
=0处可导![]()
(A)![]() 存在 (B)
存在 (B) ![]() 存在
存在
(C)![]() 存在 (D)
存在 (D)![]() 存在
存在
(4)设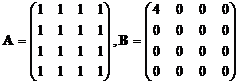 ,则
,则![]() 与
与![]()
(A)合同且相似 (B)合同但不相似
(C)不合同但相似 (D)不合同且不相似
(5)将一枚硬币重复掷![]() 次,以
次,以![]() 和
和![]() 分别表示正面向上和反面向上的次数, 则
分别表示正面向上和反面向上的次数, 则![]() 和
和![]() 相关系数为
相关系数为
(A) -1 (B)0
(C)![]() (D)1
(D)1
三、(本题满分6分)
求![]() .
.
四、(本题满分6分)
设函数![]() 在点
在点![]() 可微,且
可微,且![]() ,
,![]() ,求
,求![]() .
.
五、(本题满分8分)
设![]()
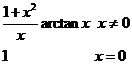 ,将
,将![]() 展开成
展开成![]() 的幂级数,并求
的幂级数,并求![]() 的和.
的和.
六、(本题满分7分)
计算![]() ,其中
,其中![]() 是平面
是平面 ![]() 与柱面
与柱面![]() 的交线,从
的交线,从![]() 轴正向看去
轴正向看去![]() 为逆时针方向.
为逆时针方向.
七、(本题满分7分)
设![]() 在
在![]() 内具有二阶连续导数且
内具有二阶连续导数且![]() .证明:
.证明:
(1)对于![]() ,存在惟一的
,存在惟一的![]() ,使
,使 ![]() =
=![]() +
+![]() 成立.
成立.
(2)![]() .
.
八、(本题满分8分)
设有一高度为![]() 为时间)的雪堆在融化过程,其侧面满足方程
为时间)的雪堆在融化过程,其侧面满足方程![]() (设长度单位为厘米,时间单位为小时),已知体积减少的速率与侧面积成正比(系数为0.9),问高度为130厘米的雪堆全部融化需多少时间?
(设长度单位为厘米,时间单位为小时),已知体积减少的速率与侧面积成正比(系数为0.9),问高度为130厘米的雪堆全部融化需多少时间?
九、(本题满分6分)
设![]() 为线性方程组
为线性方程组![]() 的一个基础解系,
的一个基础解系,
![]() ,
,
其中![]() 为实常数,试问
为实常数,试问![]() 满足什么条件时
满足什么条件时![]() 也为
也为![]() 的一个基础解系?
的一个基础解系?
十、(本题满分8分)
已知三阶矩阵![]() 和三维向量
和三维向量![]() ,使得
,使得![]() 线性无关,且满足
线性无关,且满足![]() .
.
(1)记![]() 求
求![]() 使
使![]() .
.
(2)计算行列式![]() .
.
十一、(本题满分7分)
设某班车起点站上客人数![]() 服从参数为
服从参数为![]() 的泊松分布,每位乘客在中途下车的概率为
的泊松分布,每位乘客在中途下车的概率为![]() 且中途下车与否相互独立.
且中途下车与否相互独立.![]() 为中途下车的人数,求:
为中途下车的人数,求:
(1)在发车时有![]() 个乘客的条件下,中途有
个乘客的条件下,中途有![]() 人下车的概率.
人下车的概率.
(2)二维随机变量![]() 的概率分布.
的概率分布.
十二、(本题满分7分)
设![]() 抽取简单随机样本
抽取简单随机样本![]()
样本均值![]() ,
,![]() ,求
,求![]()
2002年全国硕士研究生入学统一考试
数学(一)试卷
一、填空题(本题共5小题,每小题3分,满分15分.把答案填在题中横线上)
(1)![]() = _____________.
= _____________.
(2)已知![]() ,则
,则![]() =_____________.
=_____________.
(3)![]() 满足初始条件
满足初始条件![]() 的特解是_____________.
的特解是_____________.
(4)已知实二次型![]() 经正交变换可化为标准型
经正交变换可化为标准型![]() ,则
,则![]() =_____________.
=_____________.
(5)设随机变量![]() ,且二次方程
,且二次方程![]() 无实根的概率为0.5,则
无实根的概率为0.5,则![]() =_____________.
=_____________.
二、选择题(本题共5小题,每小题3分,满分15分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)
(1)考虑二元函数![]() 的四条性质:
的四条性质:
①![]() 在点
在点![]() 处连续, ②
处连续, ②![]() 在点
在点![]() 处的一阶偏导数连续,
处的一阶偏导数连续,
③![]() 在点
在点![]() 处可微, ④
处可微, ④![]() 在点
在点![]() 处的一阶偏导数存在.
处的一阶偏导数存在.
则有:
(A)②![]() ③
③![]() ① (B)③
① (B)③![]() ②
②![]() ①
①
(C)③![]() ④
④![]() ① (D)③
① (D)③![]() ①
①![]() ④
④
(2)设![]() ,且
,且![]() ,则级数
,则级数![]() 为
为
(A)发散 (B)绝对收敛
(C)条件收敛 (D)收敛性不能判定.
(3)设函数![]() 在
在![]() 上有界且可导,则
上有界且可导,则
(A)当![]() 时,必有
时,必有![]() (B)当
(B)当![]() 存在时,必有
存在时,必有![]()
(C) 当![]() 时,必有
时,必有![]() (D) 当
(D) 当![]() 存在时,必有
存在时,必有![]() .
.
(4)设有三张不同平面,其方程为![]() (
(![]() )它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为
)它们所组成的线性方程组的系数矩阵与增广矩阵的秩都为2,则这三张平面可能的位置关系为

(5)设![]() 和
和![]() 是相互独立的连续型随机变量,它们的密度函数分别为
是相互独立的连续型随机变量,它们的密度函数分别为![]() 和
和![]() ,分布函数分别为
,分布函数分别为![]() 和
和![]() ,则
,则
(A)![]() +
+![]() 必为密度函数 (B)
必为密度函数 (B) ![]()
![]() 必为密度函数
必为密度函数
(C)![]() +
+![]() 必为某一随机变量的分布函数 (D)
必为某一随机变量的分布函数 (D) ![]()
![]() 必为某一随机变量的分布函数.
必为某一随机变量的分布函数.
三、(本题满分6分)
设函数![]() 在
在![]() 的某邻域具有一阶连续导数,且
的某邻域具有一阶连续导数,且![]() ,当
,当![]() 时,若
时,若![]() ,试求
,试求![]() 的值.
的值.
四、(本题满分7分)
已知两曲线![]() 与
与![]() 在点
在点![]() 处的切线相同.求此切线的方程,并求极限
处的切线相同.求此切线的方程,并求极限![]() .
.
五、(本题满分7分)
计算二重积分![]() ,其中
,其中![]() .
.
六、(本题满分8分)
设函数![]() 在
在![]() 上具有一阶连续导数,
上具有一阶连续导数,![]() 是上半平面(
是上半平面(![]() >0)内的有向分段光滑曲线,起点为(
>0)内的有向分段光滑曲线,起点为(![]() ),终点为(
),终点为(![]() ).
).
记![]() ,
,
(1)证明曲线积分![]() 与路径
与路径![]() 无关.
无关.
(2)当![]() 时,求
时,求![]() 的值.
的值.
七、(本题满分7分)
(1)验证函数![]() (
(![]() )满足微分方程
)满足微分方程![]() .
.
(2)求幂级数![]() 的和函数.
的和函数.
八、(本题满分7分)
设有一小山,取它的底面所在的平面为![]() 面,其底部所占的区域为
面,其底部所占的区域为![]() ,小山的高度函数为
,小山的高度函数为![]()
![]() .
.
(1)设![]() 为区域
为区域![]() 上一点,问
上一点,问![]() 在该点沿平面上何方向的方向导数最大?若此方向的方向导数为
在该点沿平面上何方向的方向导数最大?若此方向的方向导数为![]() ,写出
,写出![]() 的表达式.
的表达式.
(2)现欲利用此小山开展攀岩活动,为此需要在山脚下寻找一山坡最大的点作为攀登的起点.也就是说要在![]() 的边界线上找出使(1)中
的边界线上找出使(1)中![]() 达到最大值的点.试确定攀登起点的位置.
达到最大值的点.试确定攀登起点的位置.
九、(本题满分6分)
已知四阶方阵![]() ,
, ![]() 均为四维列向量,其中
均为四维列向量,其中![]() 线性无关,
线性无关,![]() .若
.若![]() ,求线性方程组
,求线性方程组![]() 的通解.
的通解.
十、(本题满分8分)
设![]() 为同阶方阵,
为同阶方阵,
(1)若![]() 相似,证明
相似,证明![]() 的特征多项式相等.
的特征多项式相等.
(2)举一个二阶方阵的例子说明(1)的逆命题不成立.
(3)当![]() 为实对称矩阵时,证明(1)的逆命题成立.
为实对称矩阵时,证明(1)的逆命题成立.
十一、(本题满分7分)
设维随机变量![]() 的概率密度为
的概率密度为
![]()
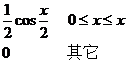
对![]() 独立地重复观察4次,用
独立地重复观察4次,用![]() 表示观察值大于
表示观察值大于![]() 的次数,求
的次数,求![]() 的数学期望.
的数学期望.
十二、(本题满分7分)
设总体![]() 的概率分布为
的概率分布为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
其中![]() (
(![]() )是未知参数,利用总体
)是未知参数,利用总体![]() 的如下样本值
的如下样本值
3,1,3,0,3,1,2,3.
求![]() 的矩估计和最大似然估计值.
的矩估计和最大似然估计值.
2003年全国硕士研究生入学统一考试
数学(一)试卷
一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上)
(1)![]() = .
= .
(2)曲面![]() 与平面
与平面![]() 平行的切平面的方程是 .
平行的切平面的方程是 .
(3)设![]() ,则
,则![]() = .
= .
(4)从![]() 的基
的基![]() 到基
到基![]() 的过渡矩阵为 .
的过渡矩阵为 .
(5)设二维随机变量![]() 的概率密度为
的概率密度为![]()
![]()
![]() ,则
,则![]() .
.
(6)已知一批零件的长度![]() (单位:cm)服从正态分布
(单位:cm)服从正态分布![]() ,从中随机地抽取16个零件,得到长度的平均值为40 (cm),则
,从中随机地抽取16个零件,得到长度的平均值为40 (cm),则![]() 的置信度为0.95的置信区间是 .
的置信度为0.95的置信区间是 .
(注:标准正态分布函数值![]()
二、选择题(本题共6小题,每小题4分,满分24分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)
(1)设函数 (A)一个极小值点和两个极大值点 (B)两个极小值点和一个极大值点 (C)两个极小值点和两个极大值点 (D)三个极小值点和一个极大值点
|
|
(2)设![]() 均为非负数列,且
均为非负数列,且![]() ,
,![]() ,
,![]() ,则必有
,则必有
(A)![]() 对任意
对任意![]() 成立 (B)
成立 (B)![]() 对任意
对任意![]() 成立
成立
(C)极限![]() 不存在 (D)极限
不存在 (D)极限![]() 不存在
不存在
(3)已知函数![]() 在点
在点![]() 的某个邻域内连续,且
的某个邻域内连续,且![]() ,则
,则
(A)点![]() 不是
不是![]() 的极值点
的极值点
(B)点![]() 是
是![]() 的极大值点
的极大值点
(C)点![]() 是
是![]() 的极小值点
的极小值点
(D)根据所给条件无法判断点![]() 是否为
是否为![]() 的极值点
的极值点
(4)设向量组I:![]() 可由向量组II:
可由向量组II:![]() 线性表示,则
线性表示,则
(A)当![]() 时,向量组II必线性相关 (B)当
时,向量组II必线性相关 (B)当![]() 时,向量组II必线性相关
时,向量组II必线性相关
(C)当![]() 时,向量组I必线性相关 (D)当
时,向量组I必线性相关 (D)当![]() 时,向量组I必线性相关
时,向量组I必线性相关
(5)设有齐次线性方程组![]() 和
和![]() ,其中
,其中![]() 均为
均为![]() 矩阵,现有4个命题:
矩阵,现有4个命题:
① 若![]() 的解均是
的解均是![]() 的解,则秩
的解,则秩![]() 秩
秩![]()
② 若秩![]() 秩
秩![]() ,则
,则![]() 的解均是
的解均是![]() 的解
的解
③ 若![]() 与
与![]() 同解,则秩
同解,则秩![]() 秩
秩![]()
④ 若秩![]() 秩
秩![]() , 则
, 则![]() 与
与![]() 同解
同解
以上命题中正确的是
(A)①② (B)①③
(C)②④ (D)③④
(6)设随机变量![]() ,则
,则
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
三、(本题满分10分)
过坐标原点作曲线![]() 的切线,该切线与曲线
的切线,该切线与曲线![]() 及
及![]() 轴围成平面图形
轴围成平面图形![]() .
.
(1)求![]() 的面积
的面积![]() .
.
(2)求![]() 绕直线
绕直线![]() 旋转一周所得旋转体的体积
旋转一周所得旋转体的体积![]() .
.
四、(本题满分12分)
将函数![]() 展开成
展开成![]() 的幂级数,并求级数
的幂级数,并求级数![]() 的和.
的和.
五 、(本题满分10分)
已知平面区域![]() ,
,![]() 为
为![]() 的正向边界.试证:
的正向边界.试证:
(1)![]() .
.
(2)![]()
六 、(本题满分10分)
某建筑工程打地基时,需用汽锤将桩打进土层.汽锤每次击打,都将克服土层对桩的阻力而作功.设土层对桩的阻力的大小与桩被打进地下的深度成正比(比例系数为![]() ).汽锤第一次击打将桩打进地下
).汽锤第一次击打将桩打进地下![]() m.根据设计方案,要求汽锤每次击打桩时所作的功与前一次击打时所作的功之比为常数
m.根据设计方案,要求汽锤每次击打桩时所作的功与前一次击打时所作的功之比为常数![]() .问
.问
(1)汽锤击打桩3次后,可将桩打进地下多深?
(2)若击打次数不限,汽锤至多能将桩打进地下多深?
(注:m表示长度单位米.)
七 、(本题满分12分)
设函数![]() 在
在![]() 内具有二阶导数,且
内具有二阶导数,且![]() 是
是![]() 的反函数.
的反函数.
(1)试将![]() 所满足的微分方程
所满足的微分方程![]() 变换为
变换为![]() 满足的微分方程.
满足的微分方程.
(2)求变换后的微分方程满足初始条件![]() 的解.
的解.
八 、(本题满分12分)
设函数![]() 连续且恒大于零,
连续且恒大于零,
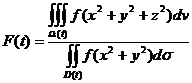 ,
, ,
,
其中![]() ,
,![]()
(1)讨论![]() 在区间
在区间![]() 内的单调性.
内的单调性.
(2)证明当![]() 时,
时,![]()
九 、(本题满分10分)
设矩阵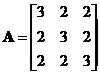 ,
,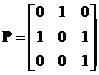 ,
,![]() ,求
,求![]() 的特征值与特征向量,其中
的特征值与特征向量,其中![]() 为
为![]() 的伴随矩阵,
的伴随矩阵,![]() 为3阶单位矩阵.
为3阶单位矩阵.
十 、(本题满分8分)
已知平面上三条不同直线的方程分别为
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() .
.
试证这三条直线交于一点的充分必要条件为![]()
十一 、(本题满分10分)
已知甲、乙两箱中装有同种产品,其中甲箱中装有3件合格品和3件次品,乙箱中仅装有3件合格品. 从甲箱中任取3件产品放入乙箱后,求:
(1)乙箱中次品件数的数学期望.
(2)从乙箱中任取一件产品是次品的概率.
十二 、(本题满分8分)
设总体![]() 的概率密度为
的概率密度为
![]()
![]()
![]()
其中![]() 是未知参数. 从总体
是未知参数. 从总体![]() 中抽取简单随机样本
中抽取简单随机样本![]() ,记
,记![]()
(1)求总体![]() 的分布函数
的分布函数![]() .
.
(2)求统计量![]() 的分布函数
的分布函数![]() .
.
(3)如果用![]() 作为
作为![]() 的估计量,讨论它是否具有无偏性.
的估计量,讨论它是否具有无偏性.
2004年全国硕士研究生入学统一考试
数学(一)试卷
一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上)
(1)曲线![]() 上与直线
上与直线![]() 垂直的切线方程为__________ .
垂直的切线方程为__________ .
(2)已知![]() ,且
,且![]() ,则
,则![]() =__________ .
=__________ .
(3)设![]() 为正向圆周
为正向圆周![]() 在第一象限中的部分,则曲线积分
在第一象限中的部分,则曲线积分![]() 的值为__________.
的值为__________.
(4)欧拉方程![]() 的通解为__________ .
的通解为__________ .
(5)设矩阵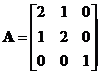 ,矩阵
,矩阵![]() 满足
满足![]() ,其中
,其中![]() 为
为![]() 的伴随矩阵,
的伴随矩阵,![]() 是单位矩阵,则
是单位矩阵,则![]() =__________ .
=__________ .
(6)设随机变量![]() 服从参数为
服从参数为![]() 的指数分布,则
的指数分布,则![]() = __________ .
= __________ .
二、选择题(本题共8小题,每小题4分,满分32分.每小题给出的四个选项中,只有一个符合题目要求,把所选项前的字母填在题后的括号内)
(7)把![]() 时的无穷小量
时的无穷小量![]() ,使排在后面的是前一个的高阶无穷小,则正确的排列次序是
,使排在后面的是前一个的高阶无穷小,则正确的排列次序是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(8)设函数![]() 连续,且
连续,且![]() 则存在
则存在![]() ,使得
,使得
(A)![]() 在(0,
在(0,![]() 内单调增加 (B)
内单调增加 (B)![]() 在
在![]() 内单调减少
内单调减少
(C)对任意的![]() 有
有![]() (D)对任意的
(D)对任意的![]() 有
有![]()
(9)设![]() 为正项级数,下列结论中正确的是
为正项级数,下列结论中正确的是
(A)若![]() =0,则级数
=0,则级数![]() 收敛
收敛
(B)若存在非零常数![]() ,使得
,使得![]() ,则级数
,则级数![]() 发散
发散
(C)若级数![]() 收敛,则
收敛,则![]()
(D)若级数![]() 发散, 则存在非零常数
发散, 则存在非零常数![]() ,使得
,使得![]()
(10)设![]() 为连续函数,
为连续函数,![]() ,则
,则![]() 等于
等于
(A)![]() (B)
(B)![]()
(C)![]() (D) 0
(D) 0
(11)设![]() 是3阶方阵,将
是3阶方阵,将![]() 的第1列与第2列交换得
的第1列与第2列交换得![]() ,再把
,再把![]() 的第2列加到第3列得
的第2列加到第3列得![]() ,则满足
,则满足![]() 的可逆矩阵
的可逆矩阵![]() 为
为
(A) (B)
(B)
(C) (D)
(D)
(12)设![]() 为满足
为满足![]() 的任意两个非零矩阵,则必有
的任意两个非零矩阵,则必有
(A)![]() 的列向量组线性相关
的列向量组线性相关![]() 的行向量组线性相关
的行向量组线性相关
(B)![]() 的列向量组线性相关
的列向量组线性相关![]() 的列向量组线性相关
的列向量组线性相关
(C)![]() 的行向量组线性相关
的行向量组线性相关![]() 的行向量组线性相关
的行向量组线性相关
(D)![]() 的行向量组线性相关
的行向量组线性相关![]() 的列向量组线性相关
的列向量组线性相关
(13)设随机变量![]() 服从正态分布
服从正态分布![]() 对给定的
对给定的![]() ,数
,数![]() 满足
满足![]() ,若
,若![]() ,则
,则![]() 等于
等于
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D) ![]()
(14)设随机变量![]() 独立同分布,且其方差为
独立同分布,且其方差为![]() 令
令![]() ,则
,则
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
三、解答题(本题共9小题,满分94分.解答应写出文字说明、证明过程或演算步骤)
(15)(本题满分12分)
设![]() ,证明
,证明![]() .
.
(16)(本题满分11分)
某种飞机在机场降落时,为了减少滑行距离,在触地的瞬间,飞机尾部张开减速伞,以增大阻力,使飞机迅速减速并停下.
现有一质量为9000kg的飞机,着陆时的水平速度为700km/h 经测试,减速伞打开后,飞机所受的总阻力与飞机的速度成正比(比例系数为![]() 问从着陆点算起,飞机滑行的最长距离是多少?
问从着陆点算起,飞机滑行的最长距离是多少?
(注:kg表示千克,km/h表示千米/小时)
(17)(本题满分12分)
计算曲面积分![]() 其中
其中![]() 是曲面
是曲面![]() 的上侧.
的上侧.
(18)(本题满分11分)
设有方程![]() ,其中
,其中![]() 为正整数.证明此方程存在惟一正实根
为正整数.证明此方程存在惟一正实根![]() ,并证明当
,并证明当![]() 时,级数
时,级数![]() 收敛.
收敛.
(19)(本题满分12分)
设![]() 是由
是由![]() 确定的函数,求
确定的函数,求![]() 的极值点和极值.
的极值点和极值.
(20)(本题满分9分)
设有齐次线性方程组
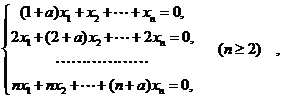
试问![]() 取何值时,该方程组有非零解,并求出其通解.
取何值时,该方程组有非零解,并求出其通解.
(21)(本题满分9分)
设矩阵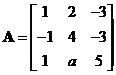 的特征方程有一个二重根,求
的特征方程有一个二重根,求![]() 的值,并讨论
的值,并讨论![]() 是否可相似对角化.
是否可相似对角化.
(22)(本题满分9分)
设![]() 为随机事件,且
为随机事件,且![]() ,令
,令
![]()
![]()
求:(1)二维随机变量![]() 的概率分布.
的概率分布.
(2)![]() 和
和![]() 的相关系数
的相关系数![]()
(23)(本题满分9分)
设总体![]() 的分布函数为
的分布函数为
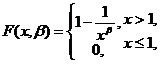
其中未知参数![]() 为来自总体
为来自总体![]() 的简单随机样本,
的简单随机样本,
求:(1)![]() 的矩估计量.
的矩估计量.
(2)![]() 的最大似然估计量.
的最大似然估计量.
2005年全国硕士研究生入学统一考试
数学(一)试卷
一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上)
(1)曲线![]() 的斜渐近线方程为 _____________.
的斜渐近线方程为 _____________.
(2)微分方程![]() 满足
满足![]() 的解为____________.
的解为____________.
(3)设函数![]() ,单位向量
,单位向量![]() ,则
,则![]() =.________.
=.________.
(4)设![]() 是由锥面
是由锥面![]() 与半球面
与半球面![]() 围成的空间区域,
围成的空间区域,![]() 是
是![]() 的整个边界的外侧,则
的整个边界的外侧,则![]() ____________.
____________.
(5)设![]() 均为3维列向量,记矩阵
均为3维列向量,记矩阵
![]() ,
,![]() ,
,
如果![]() ,那么
,那么![]() .
.
(6)从数1,2,3,4中任取一个数,记为![]() , 再从
, 再从![]() 中任取一个数,记为
中任取一个数,记为![]() , 则
, 则![]() =____________.
=____________.
二、选择题(本题共8小题,每小题4分,满分32分.每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)
(7)设函数![]() ,则
,则![]() 在
在![]() 内
内
(A)处处可导 (B)恰有一个不可导点
(C)恰有两个不可导点 (D)至少有三个不可导点
(8)设![]() 是连续函数
是连续函数![]() 的一个原函数,
的一个原函数,![]() 表示
表示![]() 的充分必要条件是
的充分必要条件是![]() 则必有
则必有
(A)![]() 是偶函数
是偶函数![]() 是奇函数 (B)
是奇函数 (B)![]() 是奇函数
是奇函数![]() 是偶函数
是偶函数
(C)![]() 是周期函数
是周期函数![]() 是周期函数 (D)
是周期函数 (D)![]() 是单调函数
是单调函数![]() 是单调函数
是单调函数
(9)设函数![]() , 其中函数
, 其中函数![]() 具有二阶导数,
具有二阶导数,![]() 具有一阶导数,则必有
具有一阶导数,则必有
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(10)设有三元方程![]() ,根据隐函数存在定理,存在点
,根据隐函数存在定理,存在点![]() 的一个邻域,在此邻域内该方程
的一个邻域,在此邻域内该方程
(A)只能确定一个具有连续偏导数的隐函数![]()
(B)可确定两个具有连续偏导数的隐函数![]() 和
和![]()
(C)可确定两个具有连续偏导数的隐函数![]() 和
和![]()
(D)可确定两个具有连续偏导数的隐函数![]() 和
和![]()
(11)设![]() 是矩阵
是矩阵![]() 的两个不同的特征值,对应的特征向量分别为
的两个不同的特征值,对应的特征向量分别为![]() ,则
,则![]() ,
,![]() 线性无关的充分必要条件是
线性无关的充分必要条件是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(12)设![]() 为
为![]() 阶可逆矩阵,交换
阶可逆矩阵,交换![]() 的第1行与第2行得矩阵
的第1行与第2行得矩阵![]() 分别为
分别为![]() 的伴随矩阵,则
的伴随矩阵,则
(A)交换![]() 的第1列与第2列得
的第1列与第2列得![]() (B)交换
(B)交换![]() 的第1行与第2行得
的第1行与第2行得![]()
(C)交换![]() 的第1列与第2列得
的第1列与第2列得![]() (D)交换
(D)交换![]() 的第1行与第2行得
的第1行与第2行得![]()
(13)设二维随机变量![]() 的概率分布为
的概率分布为
X Y | 0 | 1 |
0 | 0.4 |
|
1 |
| 0.1 |
已知随机事件![]() 与
与![]() 相互独立,则
相互独立,则
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(14)设![]() 为来自总体
为来自总体![]() 的简单随机样本,
的简单随机样本,![]() 为样本均值,
为样本均值,![]() 为样本方差,则
为样本方差,则
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)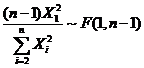
三 、解答题(本题共9小题,满分94分.解答应写出文字说明、证明过程或演算步骤)
(15)(本题满分11分)
设![]() ,
,![]() 表示不超过
表示不超过![]() 的最大整数. 计算二重积分
的最大整数. 计算二重积分![]()
(16)(本题满分12分)
求幂级数![]() 的收敛区间与和函数
的收敛区间与和函数![]() .
.
(17)(本题满分11分)
如图,曲线 |
|
(18)(本题满分12分)
已知函数![]() 在
在![]() 上连续,在
上连续,在![]() 内可导,且
内可导,且![]() . 证明:
. 证明:
(1)存在![]() 使得
使得![]() .
.
(2)存在两个不同的点![]() ,使得
,使得![]()
(19)(本题满分12分)
设函数![]() 具有连续导数,在围绕原点的任意分段光滑简单闭曲线
具有连续导数,在围绕原点的任意分段光滑简单闭曲线![]() 上,曲线积分
上,曲线积分![]() 的值恒为同一常数.
的值恒为同一常数.
(1)证明:对右半平面![]() 内的任意分段光滑简单闭曲线
内的任意分段光滑简单闭曲线![]() 有
有![]() .
.
(2)求函数![]() 的表达式.
的表达式.
(20)(本题满分9分)
已知二次型![]() 的秩为2.
的秩为2.
(1)求![]() 的值;
的值;
(2)求正交变换![]() ,把
,把![]() 化成标准形.
化成标准形.
(3)求方程![]() =0的解.
=0的解.
(21)(本题满分9分)
已知3阶矩阵![]() 的第一行是
的第一行是![]() 不全为零,矩阵
不全为零,矩阵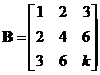 (
(![]() 为常数),且
为常数),且![]() ,求线性方程组
,求线性方程组![]() 的通解.
的通解.
(22)(本题满分9分)
设二维随机变量![]() 的概率密度为
的概率密度为
![]()
![]()
![]()
求:(1)![]() 的边缘概率密度
的边缘概率密度![]() .
.
(2)![]() 的概率密度
的概率密度![]()
(23)(本题满分9分)
设![]() 为来自总体
为来自总体![]() 的简单随机样本,
的简单随机样本,![]() 为样本均值,记
为样本均值,记![]()
求:(1)![]() 的方差
的方差![]() .
.
(2)![]() 与
与![]() 的协方差
的协方差![]()
2006年全国硕士研究生入学统一考试
数学(一)试卷
一、填空题(本题共6小题,每小题4分,满分24分.把答案填在题中横线上)
(1)![]() .
.
(2)微分方程![]() 的通解是 .
的通解是 .
(3)设![]() 是锥面
是锥面![]() (
(![]() )的下侧,则
)的下侧,则![]() .
.
(4)点![]() 到平面
到平面![]() 的距离
的距离![]() = .
= .
(5)设矩阵![]() ,
,![]() 为2阶单位矩阵,矩阵
为2阶单位矩阵,矩阵![]() 满足
满足![]() ,则
,则![]() = .
= .
(6)设随机变量![]() 与
与![]() 相互独立,且均服从区间
相互独立,且均服从区间![]() 上的均匀分布,则
上的均匀分布,则![]() = .
= .
二、选择题(本题共8小题,每小题4分,满分32分. 每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)
(7)设函数![]() 具有二阶导数,且
具有二阶导数,且![]() ,
,![]() 为自变量
为自变量![]() 在
在![]() 处的增量,
处的增量,![]() 与
与![]() 分别为
分别为![]() 在点
在点![]() 处对应的增量与微分,若
处对应的增量与微分,若![]() ,则
,则
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(8)设![]() 为连续函数,则
为连续函数,则![]() 等于
等于
(A)![]() (B)
(B)![]()
(C)![]() (C)
(C)![]()
(9)若级数![]() 收敛,则级数
收敛,则级数
(A)![]() 收敛 (B)
收敛 (B)![]() 收敛
收敛
(C)![]() 收敛 (D)
收敛 (D)![]() 收敛
收敛
(10)设![]() 与
与![]() 均为可微函数,且
均为可微函数,且![]() .已知
.已知![]() 是
是![]() 在约束条件
在约束条件![]() 下的一个极值点,下列选项正确的是
下的一个极值点,下列选项正确的是
(A)若![]() ,则
,则![]() (B)若
(B)若![]() ,则
,则![]()
(C)若![]() ,则
,则![]() (D)若
(D)若![]() ,则
,则![]()
(11)设![]() 均为
均为![]() 维列向量,
维列向量,![]() 是
是![]() 矩阵,下列选项正确的是
矩阵,下列选项正确的是
(A)若![]() 线性相关,则
线性相关,则![]() 线性相关
线性相关
(B)若![]() 线性相关,则
线性相关,则![]() 线性无关
线性无关
(C)若![]() 线性无关,则
线性无关,则![]() 线性相关
线性相关
(D)若![]() 线性无关,则
线性无关,则![]() 线性无关.
线性无关.
(12)设![]() 为3阶矩阵,将
为3阶矩阵,将![]() 的第2行加到第1行得
的第2行加到第1行得![]() ,再将
,再将![]() 的第1列的-1倍加到第2列得
的第1列的-1倍加到第2列得![]() ,记
,记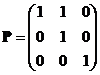 ,则
,则
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(13)设![]() 为随机事件,且
为随机事件,且![]() ,则必有
,则必有
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(14)设随机变量![]() 服从正态分布
服从正态分布![]() ,
,![]() 服从正态分布
服从正态分布![]() ,
,
且![]() 则
则
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
三、解答题(本题共9小题,满分94分.解答应写出文字说明、证明过程或演算步骤)
(15)(本题满分10分)
设区域D=![]() ,计算二重积分
,计算二重积分![]() .
.
(16)(本题满分12分)
设数列![]() 满足
满足![]() .
.
求:(1)证明![]() 存在,并求之.
存在,并求之.
(2)计算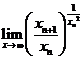 .
.
(17)(本题满分12分)
将函数![]() 展开成
展开成![]() 的幂级数.
的幂级数.
(18)(本题满分12分)
设函数![]()
![]() 满足等式
满足等式![]() .
.
(1)验证![]() .
.
(2)若![]() 求函数
求函数![]() 的表达式.
的表达式.
(19)(本题满分12分)
设在上半平面![]() 内,数
内,数![]() 是有连续偏导数,且对任意的
是有连续偏导数,且对任意的![]() 都有
都有
![]() .
.
证明: 对![]() 内的任意分段光滑的有向简单闭曲线
内的任意分段光滑的有向简单闭曲线![]() ,都有
,都有![]() .
.
(20)(本题满分9分)
已知非齐次线性方程组

有3个线性无关的解,
(1)证明方程组系数矩阵![]() 的秩
的秩![]() .
.
(2)求![]() 的值及方程组的通解.
的值及方程组的通解.
(21)(本题满分9分)
设3阶实对称矩阵![]() 的各行元素之和均为3,向量
的各行元素之和均为3,向量![]() 是线性方程组
是线性方程组![]() 的两个解.
的两个解.
(1)求![]() 的特征值与特征向量.
的特征值与特征向量.
(2)求正交矩阵![]() 和对角矩阵
和对角矩阵![]() ,使得
,使得![]() .
.
(22)(本题满分9分)
随机变量![]() 的概率密度为
的概率密度为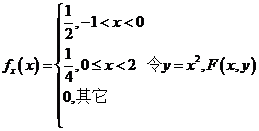 为二维随机变量
为二维随机变量![]() 的分布函数.
的分布函数.
(1)求![]() 的概率密度
的概率密度![]() .
.
(2)![]() .
.
(23)(本题满分9分)
设总体![]() 的概率密度为
的概率密度为![]()
![]()
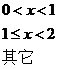 ,其中
,其中![]() 是未知参数
是未知参数![]() ,
,![]() 为来自总体
为来自总体![]() 的简单随机样本,记
的简单随机样本,记![]() 为样本值
为样本值![]() 中小于1的个数,求
中小于1的个数,求![]() 的最大似然估计.
的最大似然估计.
2007年全国硕士研究生入学统一考试
数学(一)试卷
一、选择题(本题共10小题,每小题4分,满分40分,在每小题给的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后括号内)
(1)当![]() 时,与
时,与![]() 等价的无穷小量是
等价的无穷小量是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(2)曲线![]() ,渐近线的条数为
,渐近线的条数为
(A)0 (B)1
(C)2 (D)3
(3)如图,连续函数 |
|
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(4)设函数![]() 在
在![]() 处连续,下列命题错误的是
处连续,下列命题错误的是
(A)若![]() 存在,则
存在,则![]() (B)若
(B)若![]() 存在,则
存在,则![]()
(C)若![]() 存在,则
存在,则![]() (D)若
(D)若![]() 存在,则
存在,则![]()
(5)设函数![]() 在(0, +
在(0, +![]() )上具有二阶导数,且
)上具有二阶导数,且![]() , 令
, 令![]() 则下列结论正确的是
则下列结论正确的是
(A)若![]() ,则{
,则{![]() }必收敛 (B)若
}必收敛 (B)若![]() ,则{
,则{![]() }必发散
}必发散
(C)若![]() ,则{
,则{![]() }必收敛 (D)若
}必收敛 (D)若![]() ,则{
,则{![]() }必发散
}必发散
(6)设曲线![]() (
(![]() 具有一阶连续偏导数),过第2象限内的点
具有一阶连续偏导数),过第2象限内的点![]() 和第Ⅳ象限内的点
和第Ⅳ象限内的点![]() 为
为![]() 上从点
上从点![]() 到
到![]() 的一段弧,则下列小于零的是
的一段弧,则下列小于零的是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(7)设向量组![]() 线性无关,则下列向量组线形相关的是
线性无关,则下列向量组线形相关的是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(8)设矩阵 ,
,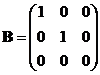 ,则
,则![]() 与
与![]()
(A)合同,且相似 (B)合同,但不相似
(C)不合同,但相似 (D)既不合同,也不相似
(9)某人向同一目标独立重复射击,每次射击命中目标的概率为![]() ,则此人第4次射击恰好第2次命中目标的概率为
,则此人第4次射击恰好第2次命中目标的概率为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(10)设随即变量![]() 服从二维正态分布,且
服从二维正态分布,且![]() 与
与![]() 不相关,
不相关,![]() ,
,![]() 分别表示
分别表示![]() 的概率密度,则在
的概率密度,则在![]() 的条件下,
的条件下,![]() 的条件概率密度
的条件概率密度![]() 为
为
(A)![]() (B)
(B)![]()
(C)![]()
![]() (D)
(D)![]()
二、填空题(11-16小题,每小题4分,共24分,请将答案写在答题纸指定位置上)
(11)![]() =_______.
=_______.
(12)设![]() 为二元可微函数,
为二元可微函数,![]() ,则
,则![]() =______.
=______.
(13)二阶常系数非齐次线性方程![]() 的通解为
的通解为![]() =____________.
=____________.
(14)设曲面![]() ,则
,则![]() =_____________.
=_____________.
(15)设矩阵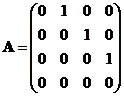 ,则
,则![]() 的秩为________.
的秩为________.
(16)在区间![]() 中随机地取两个数,则这两个数之差的绝对值小于
中随机地取两个数,则这两个数之差的绝对值小于![]() 的概率为________.
的概率为________.
三、解答题(17-24小题,共86分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤)
(17)(本题满分11分)
求函数 ![]() 在区域
在区域![]() 上的最大值和最小值.
上的最大值和最小值.
(18)(本题满分10分)
计算曲面积分![]() 其中
其中 ![]() 为曲面
为曲面![]() 的上侧.
的上侧.
(19)(本题满分11分)
设函数![]() 在
在![]() 上连续,在
上连续,在![]() 内具有二阶导数且存在相等的最大值,
内具有二阶导数且存在相等的最大值,![]() ,证明:存在
,证明:存在![]() ,使得
,使得 ![]() .
.
(20)(本题满分10分)
设幂级数 ![]() 在
在![]() 内收敛,其和函数
内收敛,其和函数![]() 满足
满足
![]()
(1)证明:![]()
(2)求![]() 的表达式.
的表达式.
(21)(本题满分11分)
设线性方程组
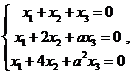
与方程
![]()
有公共解,求![]() 的值及所有公共解.
的值及所有公共解.
(22)(本题满分11分)
设3阶实对称矩阵![]() 的特征向量值
的特征向量值![]() 是
是![]() 的属于特征值
的属于特征值![]() 的一个特征向量,记
的一个特征向量,记![]() 其中
其中![]() 为3阶单位矩阵.
为3阶单位矩阵.
(1)验证![]() 是矩阵
是矩阵![]() 的特征向量,并求
的特征向量,并求![]() 的全部特征值与特征向量.
的全部特征值与特征向量.
(2)求矩阵![]() .
.
(23)(本题满分11分)
设二维随机变量![]() 的概率密度为
的概率密度为
![]()
(1)求![]()
(2)求![]() 的概率密度.
的概率密度.
(24)(本题满分11分)
设总体![]() 的概率密度为
的概率密度为
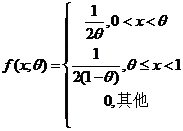
![]() 是来自总体
是来自总体![]() 的简单随机样本,
的简单随机样本,![]() 是样本均值
是样本均值
(1)求参数![]() 的矩估计量
的矩估计量![]() .
.
(2)判断![]() 是否为
是否为![]() 的无偏估计量,并说明理由.
的无偏估计量,并说明理由.
2008年全国硕士研究生入学统一考试
数学(一)试卷
一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)
(1)设函数![]() 则
则![]() 的零点个数
的零点个数
(A)0 (B)1
(C)2 (D)3
(2)函数![]() 在点
在点![]() 处的梯度等于
处的梯度等于
(A)![]() (B)-
(B)-![]()
(C)![]() (D)
(D)![]()
(3)在下列微分方程中,以![]() (
(![]() 为任意常数)为通解的是
为任意常数)为通解的是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(4)设函数![]() 在
在![]() 内单调有界,
内单调有界,![]() 为数列,下列命题正确的是
为数列,下列命题正确的是
(A)若![]() 收敛,则
收敛,则![]() 收敛 (B)若
收敛 (B)若![]() 单调,则
单调,则![]() 收敛
收敛
(C)若![]() 收敛,则
收敛,则![]() 收敛 (D)若
收敛 (D)若![]() 单调,则
单调,则![]() 收敛
收敛
(5)设![]() 为
为![]() 阶非零矩阵,
阶非零矩阵,![]() 为
为![]() 阶单位矩阵. 若
阶单位矩阵. 若![]() ,则
,则
(A)![]() 不可逆,
不可逆,![]() 不可逆 (B)
不可逆 (B)![]() 不可逆,
不可逆,![]() 可逆
可逆
(C)![]() 可逆,
可逆,![]() 可逆 (D)
可逆 (D)![]() 可逆,
可逆,![]() 不可逆
不可逆
(6)设 (A)0 (B)1 (C)2 (D)3 |
|
(7)设随机变量![]() 独立同分布且
独立同分布且![]() 分布函数为
分布函数为![]() ,则
,则![]() 分布函数为
分布函数为
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
(8)设随机变量![]() ,
,![]() 且相关系数
且相关系数![]() ,则
,则
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)
(9)微分方程![]() 满足条件
满足条件![]() 的解是
的解是![]()
![]() .
.
(10)曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(11)已知幂级数![]() 在
在![]() 处收敛,在
处收敛,在![]() 处发散,则幂级数
处发散,则幂级数![]() 的收敛域为
的收敛域为![]() .
.
(12)设曲面![]() 是
是![]() 的上侧,则
的上侧,则![]()
![]() .
.
(13)设![]() 为2阶矩阵,
为2阶矩阵,![]() 为线性无关的2维列向量,
为线性无关的2维列向量,![]() ,则
,则![]() 的非零特征值为
的非零特征值为![]() .
.
(14)设随机变量![]() 服从参数为1的泊松分布,则
服从参数为1的泊松分布,则![]()
![]() .
.
三、解答题(15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.)
(15)(本题满分10分)
求极限![]() .
.
(16)(本题满分10分)
计算曲线积分![]() ,其中
,其中![]() 是曲线
是曲线![]() 上从点
上从点![]() 到点
到点![]() 的一段.
的一段.
(17)(本题满分10分)
已知曲线 ,求曲线
,求曲线![]() 距离
距离![]() 面最远的点和最近的点.
面最远的点和最近的点.
(18)(本题满分10分)
设![]() 是连续函数,
是连续函数,
(1)利用定义证明函数![]() 可导,且
可导,且![]() .
.
(2)当![]() 是以2为周期的周期函数时,证明函数
是以2为周期的周期函数时,证明函数![]() 也是以2为周期的周期函数.
也是以2为周期的周期函数.
(19)(本题满分10分)
![]() ,用余弦级数展开,并求
,用余弦级数展开,并求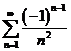 的和.
的和.
(20)(本题满分11分)
![]() ,
,![]() 为
为![]() 的转置,
的转置,![]() 为
为![]() 的转置.证明:
的转置.证明:
(1)![]() .
.
(2)若![]() 线性相关,则
线性相关,则![]() .
.
(21)(本题满分11分)
设矩阵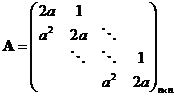 ,现矩阵
,现矩阵![]() 满足方程
满足方程![]() ,其中
,其中![]() ,
,![]() ,
,
(1)求证![]() .
.
(2)![]() 为何值,方程组有唯一解,求
为何值,方程组有唯一解,求![]() .
.
(3)![]() 为何值,方程组有无穷多解,求通解.
为何值,方程组有无穷多解,求通解.
(22)(本题满分11分)
设随机变量![]() 与
与![]() 相互独立,
相互独立,![]() 的概率分布为
的概率分布为![]() ,
,![]() 的概率密度为
的概率密度为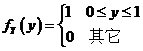 ,记
,记![]() ,
,
(1)求![]() .
.
(2)求![]() 的概率密度.
的概率密度.
(23)(本题满分11分)
设![]() 是总体为
是总体为![]() 的简单随机样本.
的简单随机样本.
记![]() ,
,![]() ,
,![]()
(1)证明![]() 是
是![]() 的无偏估计量.
的无偏估计量.
(2)当![]() 时 ,求
时 ,求![]() .
.
2009年全国硕士研究生入学统一考试
数学(一)试卷
一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)
(1)当![]() 时,
时,![]() 与
与![]() 等价无穷小,则
等价无穷小,则
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(2)如图,正方形
(A) (C)
|
|
(3)设函数![]() 在区间
在区间![]() 上的图形为
上的图形为
1
![]()
-2
0
2
3
![]()
-1
O

则函数![]() 的图形为
的图形为
(A)
![]()
0
2
3
![]()
1
-2
-1
1
(B)![]()
0
2
3
![]()
1
-2
-1
1
(C)
![]()
0
2
3
![]()
1
-1
1
(D)![]()
0
2
3
![]()
1
-2
-1
1
(4)设有两个数列![]() ,若
,若![]() ,则
,则
(A)当![]() 收敛时,
收敛时,![]() 收敛. (B)当
收敛. (B)当![]() 发散时,
发散时,![]() 发散.
发散.
(C)当![]() 收敛时,
收敛时,![]() 收敛. (D)当
收敛. (D)当![]() 发散时,
发散时,![]() 发散.
发散.
(5)设![]() 是3维向量空间
是3维向量空间![]() 的一组基,则由基
的一组基,则由基![]() 到基
到基![]() 的过渡矩阵为
的过渡矩阵为
(A)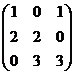 (B)
(B)
(C)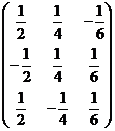 (D)
(D)
(6)设![]()
![]() 均为2阶矩阵,
均为2阶矩阵,![]() 分别为
分别为![]()
![]() 的伴随矩阵,若
的伴随矩阵,若![]() ,则分块矩阵
,则分块矩阵![]() 的伴随矩阵为
的伴随矩阵为
(A) (B)
(B)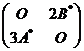
(C)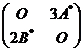 (D)
(D)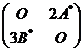
(7)设随机变量![]() 的分布函数为
的分布函数为![]() ,其中
,其中![]() 为标准正态分布函数,则
为标准正态分布函数,则![]()
(A)0 (B)0.3
(C)0.7 (D)1
(8)设随机变量![]() 与
与![]() 相互独立,且
相互独立,且![]() 服从标准正态分布
服从标准正态分布![]() ,
,![]() 的概率分布为
的概率分布为![]() ,记
,记![]() 为随机变量
为随机变量![]() 的分布函数,则函数
的分布函数,则函数![]() 的间断点个数为
的间断点个数为
(A)0 (B)1
(C)2 (D)3
二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)
(9)设函数![]() 具有二阶连续偏导数,
具有二阶连续偏导数,![]() ,则
,则![]() .
.
(10)若二阶常系数线性齐次微分方程![]() 的通解为
的通解为![]() ,则非齐次方程
,则非齐次方程![]() 满足条件
满足条件![]() 的解为
的解为![]() .
.
(11)已知曲线![]() ,则
,则![]() .
.
(12)设![]() ,则
,则![]() .
.
(13)若3维列向量![]() 满足
满足![]() ,其中
,其中![]() 为
为![]() 的转置,则矩阵
的转置,则矩阵![]() 的非零特征值为 .
的非零特征值为 .
(14)设![]() 为来自二项分布总体
为来自二项分布总体![]() 的简单随机样本,
的简单随机样本,![]() 和
和![]() 分别为样本均值和样本方差.若
分别为样本均值和样本方差.若![]() 为
为![]() 的无偏估计量,则
的无偏估计量,则![]() .
.
三、解答题(15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.)
(15)(本题满分9分)
求二元函数![]() 的极值.
的极值.
(16)(本题满分9分)
设![]() 为曲线
为曲线![]() 与
与![]() 所围成区域的面积,记
所围成区域的面积,记![]() ,求
,求![]() 与
与![]() 的值.
的值.
(17)(本题满分11分)
椭球面![]() 是椭圆
是椭圆![]() 绕
绕![]() 轴旋转而成,圆锥面
轴旋转而成,圆锥面![]() 是过点
是过点![]() 且与椭圆
且与椭圆![]() 相切的直线绕
相切的直线绕![]() 轴旋转而成.
轴旋转而成.
(1)求![]() 及
及![]() 的方程.
的方程.
(2)求![]() 与
与![]() 之间的立体体积.
之间的立体体积.
(18)(本题满分11分)
(1)证明拉格朗日中值定理:若函数![]() 在
在![]() 上连续,在
上连续,在![]() 可导,则存在
可导,则存在![]() ,使得
,使得![]() .
.
(2)证明:若函数![]() 在
在![]() 处连续,在
处连续,在![]() 内可导,且
内可导,且![]() ,则
,则![]() 存在,且
存在,且![]() .
.
(19)(本题满分10分)
计算曲面积分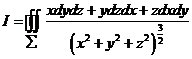 ,其中
,其中![]() 是曲面
是曲面![]() 的外侧.
的外侧.
(20)(本题满分11分)
设 ,
,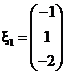
(1)求满足![]() 的
的![]() .
.![]() 的所有向量
的所有向量![]() ,
,![]() .
.
(2)对(1)中的任意向量![]() ,
,![]() 证明
证明![]() 无关.
无关.
(21)(本题满分11分)
设二次型![]() .
.
(1)求二次型![]() 的矩阵的所有特征值;
的矩阵的所有特征值;
(2)若二次型![]() 的规范形为
的规范形为![]() ,求
,求![]() 的值.
的值.
(22)(本题满分11分)
袋中有1个红色球,2个黑色球与3个白球,现有回放地从袋中取两次,每次取一球,以![]() 分别表示两次取球所取得的红球、黑球与白球的个数.
分别表示两次取球所取得的红球、黑球与白球的个数.
(1)求![]() .
.
(2)求二维随机变量![]() 概率分布.
概率分布.
(23)(本题满分11 分)
设总体![]() 的概率密度为
的概率密度为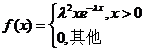 ,其中参数
,其中参数![]() 未知,
未知,![]() ,
,![]() ,…
,…![]() 是来自总体
是来自总体![]() 的简单随机样本.
的简单随机样本.
(1)求参数![]() 的矩估计量.
的矩估计量.
(2)求参数![]() 的最大似然估计量.
的最大似然估计量.
2010年全国硕士研究生入学统一考试
数学(一)试卷
一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)
(1)极限 =
=
(A)1 (B)![]()
(C)![]() (D)
(D)![]()
(2)设函数![]() 由方程
由方程![]() 确定,其中
确定,其中![]() 为可微函数,且
为可微函数,且![]() 则
则![]() =
=
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(3)设![]() 为正整数,则反常积分
为正整数,则反常积分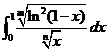 的收敛性
的收敛性
(A)仅与![]() 取值有关 (B)仅与
取值有关 (B)仅与![]() 取值有关
取值有关
(C)与![]() 取值都有关 (D)与
取值都有关 (D)与![]() 取值都无关
取值都无关
(4)![]() =
=
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(5)设![]() 为
为![]() 型矩阵
型矩阵![]() 为
为![]() 型矩阵,若
型矩阵,若![]() 则
则
(A)秩![]() 秩
秩![]() (B)秩
(B)秩![]() 秩
秩![]()
(C)秩![]() 秩
秩![]() (D)秩
(D)秩![]() 秩
秩![]()
(6)设![]() 为4阶对称矩阵,且
为4阶对称矩阵,且![]() 若
若![]() 的秩为3,则
的秩为3,则![]() 相似于
相似于
(A)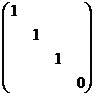 (B)
(B)
(C)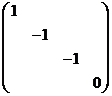 (D)
(D)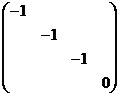
(7)设随机变量![]() 的分布函数
的分布函数![]()
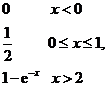 则
则![]() =
=
(A)0 (B)1
(C)![]() (D)
(D)![]()
(8)设![]() 为标准正态分布的概率密度
为标准正态分布的概率密度![]() 为
为![]() 上均匀分布的概率密度,
上均匀分布的概率密度,
![]()
![]()
![]()
![]()
为概率密度,则![]() 应满足
应满足
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
二、填空题(9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.)
(9)设![]() 求
求![]() = .
= .
(10)![]() = .
= .
(11)已知曲线![]() 的方程为
的方程为![]() 起点是
起点是![]() 终点是
终点是![]()
则曲线积分![]() = .
= .
(12)设![]() 则
则![]() 的形心的竖坐标
的形心的竖坐标![]() = .
= .
(13)设![]() 若由
若由![]() 形成的向量空间的维数是2,则
形成的向量空间的维数是2,则![]() = .
= .
(14)设随机变量![]() 概率分布为
概率分布为![]() 则
则![]() = .
= .
三、解答题(15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.)
(15)(本题满分10分)
求微分方程![]() 的通解.
的通解.
(16)(本题满分10分)
求函数![]() 的单调区间与极值.
的单调区间与极值.
(17)(本题满分10分)
(1)比较![]() 与
与![]() 的大小,说明理由.
的大小,说明理由.
(2)记![]() 求极限
求极限![]()
(18)(本题满分10分)
求幂级数![]() 的收敛域及和函数.
的收敛域及和函数.
(19)(本题满分10分)
设![]() 为椭球面
为椭球面![]() 上的动点,若
上的动点,若![]() 在点
在点![]() 的切平面与
的切平面与![]() 面垂直,求
面垂直,求![]() 点的轨迹
点的轨迹![]() 并计算曲面积分
并计算曲面积分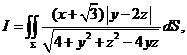 其中
其中![]() 是椭球面
是椭球面![]() 位于曲线
位于曲线![]() 上方的部分.
上方的部分.
(20)(本题满分11分)
设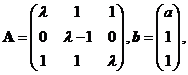 已知线性方程组
已知线性方程组![]() 存在两个不同的解.
存在两个不同的解.
(1)求![]()
(2)求方程组![]() 的通解.
的通解.
(21)(本题满分11分)
设二次型![]() 在正交变换
在正交变换![]() 下的标准形为
下的标准形为![]() 且
且![]() 的第三列为
的第三列为![]()
(1)求![]()
(2)证明![]() 为正定矩阵,其中
为正定矩阵,其中![]() 为3阶单位矩阵.
为3阶单位矩阵.
(22)(本题满分11分)
设二维随机变量![]() 的概率密度为
的概率密度为![]() 求常数及
求常数及![]() 条件概率密度
条件概率密度![]()
(23)(本题满分11 分)
设总体![]() 的概率分布为
的概率分布为
| 1 | 2 | 3 |
|
|
|
|
其中![]() 未知,以
未知,以![]() 来表示来自总体
来表示来自总体![]() 的简单随机样本(样本容量为
的简单随机样本(样本容量为![]() )中等于
)中等于![]() 的个数
的个数![]() 试求常数
试求常数![]() 使
使![]() 为
为![]() 的无偏估计量,并求
的无偏估计量,并求![]() 的方差.
的方差.
2011年全国硕士研究生入学统一考试
数学(一)试卷
一、选择题(1-8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.)
曲线![]() 的拐点是( )
的拐点是( )
A (1,0) B (2,0) C (3![]() ,0) D (4,0)
,0) D (4,0)
2、设数列![]() 单调减少,且
单调减少,且![]() 。
。![]() 无界,则幂级数
无界,则幂级数![]() 的收敛域为( )
的收敛域为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
设函数![]() 具有二阶连续的导数,且
具有二阶连续的导数,且![]() .
.![]() 。则函数
。则函数![]() 在点
在点![]() 处取得极小值的一个充分条件是( )
处取得极小值的一个充分条件是( )
A ![]() B
B ![]()
C ![]() D
D ![]()
4、设![]()
![]()
![]() ,则
,则 ![]() 的大小关系是( )
的大小关系是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
5、设A为3阶矩阵,把A的第二列加到第一列得到矩阵B ,再交换B的第二行与第3行得到单位阵E,记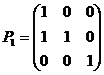 ,
,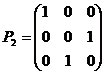 ,则A=( )
,则A=( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
6、设![]() 是4阶矩阵,
是4阶矩阵,![]() 为A的伴随矩阵。若
为A的伴随矩阵。若![]() 是
是![]() 的一个基础解系,则
的一个基础解系,则![]() 的基础解系可为( )
的基础解系可为( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
7、设![]() 为两个分布函数,且连续函数
为两个分布函数,且连续函数![]() 为相应的概率密度,则必为概率密度的是( )
为相应的概率密度,则必为概率密度的是( )
A ![]() B
B ![]() C
C ![]() D
D ![]() +
+![]()
8、设随机变量![]() 相互独立,且
相互独立,且![]() 都存在,记
都存在,记![]()
![]() ,则
,则![]() ( )
( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
二、填空题:9—14小题,每小题4分,共24分,请将答案写在答题纸指定的位置上。
9、曲线![]() 的弧长为_____________
的弧长为_____________
10、微分方程![]() 满足条件
满足条件![]() 的解为________________
的解为________________
11、设函数![]() ,则
,则![]()
12、设![]() 是柱面方程
是柱面方程![]() 与平面
与平面![]() 的交线,从
的交线,从![]() 轴正向往
轴正向往![]() 轴负向看去为逆时针方向,则曲线积分
轴负向看去为逆时针方向,则曲线积分![]()
13、若二次曲面的方程![]() ,经正交变换化为
,经正交变换化为![]() ,则
,则![]()
14、设二维随机变量![]() ,则
,则![]()
三、解答题:15—23小题,共94分.请将解答写在答题纸指定的位置上,解答应写出文字说明,证明过程或演算步骤。
15、(本题满分10分) 求极限![]()
16、(本题满分9分)
设函数![]() ,其中
,其中![]() 具有二阶连续的偏导数,函数
具有二阶连续的偏导数,函数![]() 可导且在
可导且在![]() 处取得极值
处取得极值![]() .求
.求![]()
17、(本题满分10分)
求方程![]() 的不同实根的个数,其中
的不同实根的个数,其中![]() 为参数。
为参数。
18、(本题满分10分)
①证明:对任意的正整数![]() ,都有
,都有![]() 成立;
成立;
②设![]() ,证明数列
,证明数列![]() 收敛.
收敛.
19、(本题满分11分)
已知函数![]() 具有二阶连续的偏导数,且
具有二阶连续的偏导数,且![]() ,其中
,其中![]() 计算二重积分
计算二重积分![]()
20、(本题满分11分)
设向量组![]() ,
,![]() ,
,![]() 不能由向量组
不能由向量组![]() ,
,![]() ,
,![]() 线性表示;
线性表示;
求![]() 的值;
的值;
将![]() 用
用![]() 线性表示;
线性表示;
21、(本题满分11分)
A为3阶实对称矩阵,A的秩为2,且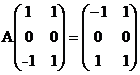
求(1)A的特征值与特征向量 (2) 矩阵A
22、(本题满分11分)
设随机变量X与Y的概率分布分别为
X | 0 | 1 |
|
|
|
Y | -1 | 0 | 1 |
|
|
|
|
且![]()
求(1)二维随机变量(X,Y)的概率分布;
(2)![]() 的概率分布
的概率分布
(3)X与Y的相关系数![]()
23、(本题满分11分)
设![]() 是来自正态总体
是来自正态总体![]() 的简单随机样本,其中
的简单随机样本,其中![]() 已知,
已知,![]() 未知.
未知.![]() 为样本均值和样本方差.
为样本均值和样本方差.
求(1)求参数![]() 的最大似然估计
的最大似然估计![]()
(2) 计算E![]() 和D
和D![]()
2012年全国硕士研究生入学统一考试
数学(一)试卷
一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
(1)曲线![]() 渐近线的条数为()
渐近线的条数为()
(A)0
(B)1
(C)2
(D)3
(2)设函数![]() ,其中
,其中![]() 为正整数,则
为正整数,则![]()
(A)![]()
(B)![]()
(C)![]()
(D)![]()
(3)如果![]() 在
在![]() 处连续,那么下列命题正确的是( )
处连续,那么下列命题正确的是( )
(A)若极限![]() 存在,则
存在,则![]() 在
在![]() 处可微
处可微
(B)若极限![]() 存在,则
存在,则![]() 在
在![]() 处可微
处可微
(C)若![]() 在
在![]() 处可微,则极限
处可微,则极限![]() 存在
存在
(D)若![]() 在
在![]() 处可微,则极限
处可微,则极限![]() 存在
存在
(4)设![]() sinxdx(k=1,2,3),则有D
sinxdx(k=1,2,3),则有D
(A)I1< I2 <I3. (B) I2< I2< I3.
(C) I1< I3 <I1, (D) I1< I2< I3.
(5)设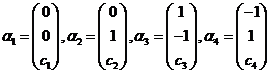 其中
其中![]() 为任意常数,则下列向量组线性相关的是( )
为任意常数,则下列向量组线性相关的是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(6)设![]() 为3阶矩阵,
为3阶矩阵,![]() 为3阶可逆矩阵,且
为3阶可逆矩阵,且 ,
,![]() ,
,![]() 则
则![]() ( )
( )
(A)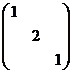 (B)
(B)
(C)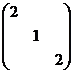 (D)
(D)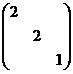
(7)设随机变量x与y相互独立,且分别服从参数为1与参数为4的指数分布,则![]() ()
()
![]()
(8)将长度为1m的木棒随机地截成两段,则两段长度的相关系数为()![]()
二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.
(9)若函数![]() 满足方程
满足方程![]() 及
及![]() ,则
,则![]() =________。
=________。
(10)![]() ________。
________。
(11)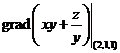 ________。
________。
(12)设![]() 则
则![]() ________。
________。
(13)设X为三维单位向量,E为三阶单位矩阵,则矩阵![]() 的秩为________。
的秩为________。
(14)设![]() 是随机事件,
是随机事件,![]() 互不相容,
互不相容,![]() ,
,![]() ,则
,则![]() ________。
________。
三、解答题:15—23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分10分)
证明:![]()
(16)(本题满分10分)
求![]() 的极值。
的极值。

(2)已知线性方程组![]() 有无穷多解,求
有无穷多解,求![]() ,并求
,并求![]() 的通解。
的通解。
(21)(本题满分10分)三阶矩阵 ,
,![]() 为矩阵
为矩阵![]() 的转置,已知
的转置,已知![]() ,且二次型
,且二次型![]() 。
。
1)求![]()
2)求二次型对应的二次型矩阵,并将二次型化为标准型,写出正交变换过程。
(22)(本题满分10分)
已知随机变量![]() 以及
以及![]() 的分布律如下表所示,
的分布律如下表所示,
X | 0 | 1 | 2 |
P | 1/2 | 1/3 | 1/6 |
Y | 0 | 1 | 2 |
P | 1/3 | 1/3 | 1/3 |
XY | 0 | 1 | 2 | 4 |
P | 7/12 | 1/3 | 0 | 1/12 |
求:(1)![]() ;
;
(2)![]() 与
与![]() .
.
(23)(本题满分11分)
设随机变量![]() 与
与![]() 相互独立且分别服从正态分布
相互独立且分别服从正态分布![]() 与
与![]() ,其中
,其中![]() 是未知参数且
是未知参数且![]() ,设
,设![]() ,
,
求![]() 的概率密度
的概率密度![]() ;
;
设![]() 为来自总体
为来自总体![]() 的简单随机样本,求
的简单随机样本,求![]() 的最大似然估计量
的最大似然估计量![]() ;
;
证明![]() 为
为![]() 的无偏估计量。
的无偏估计量。
2013硕士研究生入学考试数学一真题
已知极限![]() ,其中k,c为常数,且
,其中k,c为常数,且![]() ,则()
,则()
2.曲面![]() 在点
在点![]() 处的切平面方程为( )
处的切平面方程为( )
3.设![]() ,
,![]() ,令
,令![]() ,则( )
,则( )
A .![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4.设![]() ,
,![]() ,
,![]() ,
,![]() 为四条逆时针方向的平面曲线,记
为四条逆时针方向的平面曲线,记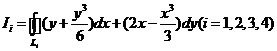 ,则
,则![]()
A. ![]() B.
B. ![]() C.
C. ![]() D
D ![]()
5.设A,B,C均为n阶矩阵,若AB=C,且B可逆,则( )
A.矩阵C的行向量组与矩阵A的行向量组等价
B矩阵C的列向量组与矩阵A的列向量组等价
C矩阵C的行向量组与矩阵B的行向量组等价
D矩阵C的列向量组与矩阵B的列向量组等价
6.矩阵 与
与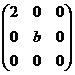 相似的充分必要条件为( )
相似的充分必要条件为( )
A. ![]() B.
B. ![]() 为任意常数
为任意常数
C. ![]() D.
D. ![]() 为任意常数
为任意常数
7.设![]() 是随机变量,且
是随机变量,且![]() ,
,![]() ,
,![]() ,
,![]() ,则( )
,则( )
A. ![]() B.
B. ![]() C.
C. ![]() D
D![]()
8.设随机变量![]() ,
,![]() ,给定
,给定![]() ,常数c满足
,常数c满足![]() ,则
,则
![]() ( )
( )
(9)设函数y=f(x)由方程y-x=ex(1-y) 确定,则![]() = 。
= 。
(10)已知y1=e3x –xe2x,y2=ex –xe2x,y3= –xe2x是某二阶常系数非齐次线性微分方程的3个解,则该方程的通解y= 。
(11)设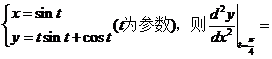 。
。
(12)![]() 。
。
(13)设A=(aij)是3阶非零矩阵,![]() 为A的行列式,Aij为aij的代数余子式.若aij+Aij=0(i,j=1,2,3),则|A|= 。
为A的行列式,Aij为aij的代数余子式.若aij+Aij=0(i,j=1,2,3),则|A|= 。
(14)设随机变量Y服从参数为1的指数分布,a为常数且大于零,则P{Y≤a+1|Y>a}=
三.解答题:
(15)(本题满分10分)
计算![]() ,其中f(x)=
,其中f(x)=![]()
(16)(本题10分)
设数列{an}满足条件:![]() S(x)是幂级数
S(x)是幂级数
![]()
(1)证明:![]()
(2)求![]()
(17)(本题满分10分)
求函数![]() .
.
(18)(本题满分10分)
设奇函数f(x)在![]() 上具有二阶导数,且f(1)=1,证明:
上具有二阶导数,且f(1)=1,证明:
(I)存在![]()
(Ⅱ)存在![]()
19.(本题满分10分)
设直线L过A(1,0,0),B(0,1,1)两点将L绕z轴旋转一周得到曲面![]() ,
,![]() 与平面
与平面![]() 所围成的立体为
所围成的立体为![]() 。
。
求曲面![]() 的方程;
的方程;
求![]() 的形心坐标。
的形心坐标。
20.(本题满分11分)
设![]() ,当a,b为何值时,存在矩阵C使得AC-CA=B,并求所有矩阵C。
,当a,b为何值时,存在矩阵C使得AC-CA=B,并求所有矩阵C。
21.(本题满分11分)
设二次型![]() ,记
,记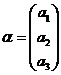 ,
,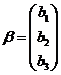 。
。
证明二次型f对应的矩阵为![]() ;
;
若![]() 正交且均为单位向量,证明f在正交变换下的标准形为
正交且均为单位向量,证明f在正交变换下的标准形为![]() 。
。
22.(本题满分11分)
设随机变量X的概率密度为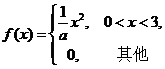 令随机变量
令随机变量
求Y的分布函数;
求概率![]() .
.
23.(本题满分11分)
设总体X的概率密度为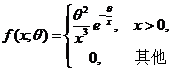 其中
其中![]() 为未知参数且大于零,
为未知参数且大于零,![]() 为来自总体X的简单随机样本。
为来自总体X的简单随机样本。
求![]() 的矩估计量;
的矩估计量;
求![]() 的最大似然估计量。
的最大似然估计量。
一、选择题:1![]() 8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
(1) 下列曲线有渐近线的是 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(2) 设函数![]() 具有二阶导数,
具有二阶导数,![]() ,则在区间
,则在区间![]() 上 ( )
上 ( )
(A) 当![]() 时,
时,![]() (B) 当
(B) 当![]() 时,
时,![]()
(C) 当![]() 时,
时,![]() (D) 当
(D) 当![]() 时,
时,![]()
(3) 设![]() 是连续函数,则
是连续函数,则![]() ( )
( )
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(4) 若![]() ,则
,则
![]() ( )
( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(5) 行列式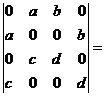 ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(6) 设![]() 均为三维向量,则对任意常数
均为三维向量,则对任意常数![]() ,向量组
,向量组![]() ,
,![]() 线性无关是向量组
线性无关是向量组![]() 线性无关的 ( )
线性无关的 ( )
(A)必要非充分条件 (B)充分非必要条件
(C)充分必要条件 (D)既非充分也非必要条件
(7) 设随机事件![]() 与
与![]() 相互独立,且
相互独立,且![]() ,
,![]() ,则
,则![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(8) 设连续性随机变量![]() 与
与![]() 相互独立,且方差均存在,
相互独立,且方差均存在,![]() 与
与![]() 的概率密度分别为
的概率密度分别为![]() 与
与
![]() ,随机变量
,随机变量![]() 的概率密度为
的概率密度为![]() ,随机变量
,随机变量![]() ,则
,则
( )
(A) ![]() ,
,![]() (B)
(B) ![]() ,
,![]()
(C) ![]() ,
,![]() (D)
(D) ![]() ,
,![]()
二、填空题:9![]() 14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.
14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.
(9) 曲面![]() 在点
在点![]() 处的切平面方程为__________.
处的切平面方程为__________.
(10) 设![]() 是周期为
是周期为![]() 的可导奇函数,且
的可导奇函数,且![]()
![]()
![]() ,则
,则![]() __________.
__________.
(11) 微分方程![]() 满足条件
满足条件![]() 的解为
的解为![]() __________.
__________.
(12) 设![]() 是柱面
是柱面![]() 与平面
与平面![]() 的交线,从
的交线,从![]() 轴正向往
轴正向往![]() 轴负向看去为逆时针方向,则曲线积分
轴负向看去为逆时针方向,则曲线积分![]() __________.
__________.
(13) 设二次型![]() 的负惯性指数是1,则
的负惯性指数是1,则![]() 的取值范围_________.
的取值范围_________.
(14) 设总体![]() 的概率密度为
的概率密度为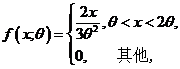 其中
其中![]() 是未知参数,
是未知参数,![]() 为来自总体
为来自总体![]() 的简单样本,若
的简单样本,若![]() ,则
,则![]() _________.
_________.
三、解答题:15~23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分10分)
求极限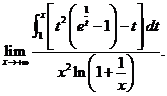
(16)(本题满分10分)
设函数![]() 由方程
由方程![]() 确定,求
确定,求![]() 的极值.
的极值.
(17)(本题满分10分)
设函数![]() 具有二阶连续导数,
具有二阶连续导数,![]() 满足
满足![]() 若
若![]() ,求
,求![]() 的表达式.
的表达式.
(18)(本题满分10分)
设![]() 为曲面
为曲面![]()
![]() 的上侧,计算曲面积分
的上侧,计算曲面积分
![]() .
.
(19)(本题满分10分)
设数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,且级数
,且级数![]() 收敛.
收敛.
(I) 证明:![]() .
.
(II) 证明:级数![]() 收敛.
收敛.
(20)(本题满分11分)
设矩阵 ,
,![]() 为三阶单位矩阵.
为三阶单位矩阵.
(I)求方程组![]() 的一个基础解系;
的一个基础解系;
(II)求满足![]() 的所有矩阵
的所有矩阵![]() .
.
(21)(本题满分11分)
证明![]() 阶矩阵
阶矩阵 与
与 相似.
相似.
(22)(本题满分11分)
设随机变量![]() 的概率分布为
的概率分布为![]() 在给定
在给定![]() 的条件下,随机变量
的条件下,随机变量![]() 服从均匀分布
服从均匀分布![]() .
.
(I)求![]() 的分布函数
的分布函数![]() ;
;
(II)求![]() .
.
(23)(本题满分11 分)
设总体![]() 的分布函数为
的分布函数为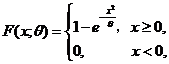 其中
其中![]() 是未知参数且大于零.
是未知参数且大于零.![]() 为来自总体
为来自总体![]() 的简单随机样本.
的简单随机样本.
(I)求![]() ,
,![]() ;
;
(II)求![]() 的最大似然估计量
的最大似然估计量![]() ;
;
(III)是否存在实数![]() ,使得对任何
,使得对任何![]() ,都有
,都有![]() ?
?
2015年全国硕士研究生入学统一考试数学(一)试题
一、选择题:1![]() 8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
(1)设函数![]() 在
在![]() 内连续,其中二阶导数
内连续,其中二阶导数![]() 的图形如图所示,则曲线
的图形如图所示,则曲线![]() 的拐点的个数为 ( )
的拐点的个数为 ( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(2)设![]() 是二阶常系数非齐次线性微分方程
是二阶常系数非齐次线性微分方程![]() 的一个特解,则 ( )
的一个特解,则 ( )
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(3) 若级数![]() 条件收敛,则
条件收敛,则 ![]() 与
与![]() 依次为幂级数
依次为幂级数![]() 的 ( )
的 ( )
(A) 收敛点,收敛点
(B) 收敛点,发散点
(C) 发散点,收敛点
(D) 发散点,发散点
(4) 设![]() 是第一象限由曲线
是第一象限由曲线![]() ,
,![]() 与直线
与直线![]() ,
,![]() 围成的平面区域,函数
围成的平面区域,函数![]() 在
在![]() 上连续,则
上连续,则![]() ( )
( )
(A) ![]()
(B)
(C) ![]()
(D) 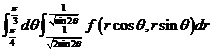
(5) 设矩阵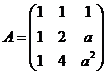 ,
,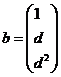 ,若集合
,若集合![]() ,则线性方程组
,则线性方程组![]() 有无穷多解的充分必要条件为 ( )
有无穷多解的充分必要条件为 ( )
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(6)设二次型![]() 在正交变换为
在正交变换为![]() 下的标准形为
下的标准形为![]() ,其中
,其中![]() ,若
,若![]() ,则
,则![]() 在正交变换
在正交变换![]() 下的标准形为 ( )
下的标准形为 ( )
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
(7) 若A,B为任意两个随机事件,则 ( )
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
(8)设随机变量![]() 不相关,且
不相关,且![]() ,则
,则![]() ( )
( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
二、填空题:9![]() 14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.
14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.
(9) ![]()
(10) ![]()
(11)若函数![]() 由方程
由方程![]() 确定,则
确定,则![]()
(12)设![]() 是由平面
是由平面![]() 与三个坐标平面平面所围成的空间区域,则
与三个坐标平面平面所围成的空间区域,则![]()
(13) ![]() 阶行列式
阶行列式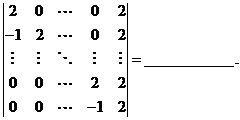
(14)设二维随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]()
三、解答题:15~23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分10分) 设函数![]() ,
,![]() ,若
,若![]() 与
与![]() 在
在![]() 是等价无穷小,求
是等价无穷小,求![]() 的值.
的值.
(16)(本题满分10分) 设函数![]() 在定义域I上的导数大于零,若对任意的
在定义域I上的导数大于零,若对任意的![]() ,由线
,由线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 及
及![]() 轴所围成区域的面积恒为4,且
轴所围成区域的面积恒为4,且![]() ,求
,求![]() 的表达式.
的表达式.
(17)(本题满分10分)
已知函数![]() ,曲线C:
,曲线C:![]() ,求
,求![]() 在曲线C上的最大方向导数.
在曲线C上的最大方向导数.
(18)(本题满分 10 分)
(I)设函数![]() 可导,利用导数定义证明
可导,利用导数定义证明![]()
(II)设函数![]() 可导,
可导,![]() ,写出
,写出![]() 的求导公式.
的求导公式.
(19)(本题满分 10 分)
已知曲线L的方程为 起点为
起点为![]() ,终点为
,终点为![]() ,计算曲线积分
,计算曲线积分![]() .
.
(20) (本题满11分)
设向量组![]() 内
内![]() 的一个基,
的一个基,![]() ,
,![]() ,
,![]() .
.
(I)证明向量组![]()
![]()
![]() 为
为![]() 的一个基;
的一个基;
(II)当k为何值时,存在非0向量![]() 在基
在基![]() 与基
与基![]()
![]()
![]() 下的坐标相同,并求所有的
下的坐标相同,并求所有的![]() .
.
(21) (本题满分11 分)
设矩阵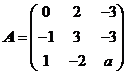 相似于矩阵
相似于矩阵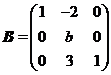 .
.
求![]() 的值;
的值;
(II)求可逆矩阵![]() ,使
,使![]() 为对角矩阵..
为对角矩阵..
(22) (本题满分11 分) 设随机变量![]() 的概率密度为
的概率密度为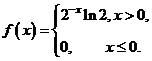
对![]() 进行独立重复的观测,直到2个大于3的观测值出现的停止.记
进行独立重复的观测,直到2个大于3的观测值出现的停止.记![]() 为观测次数.
为观测次数.
(I)求![]() 的概率分布;
的概率分布;
(II)求![]()
(23) (本题满分 11 分)设总体X的概率密度为:

其中![]() 为未知参数,
为未知参数,![]() 为来自该总体的简单随机样本.
为来自该总体的简单随机样本.
(I)求![]() 的矩估计量.
的矩估计量.
(II)求![]() 的最大似然估计量.
的最大似然估计量.
2016考研数学(一)真题
一、选择题:1 8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.


二、填空题:9 14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.

三、解答题:15~23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.


(23)(本题满分11分)
