

一、选择题:1![]() 8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
(1) 下列反常积分收敛的是 ( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
【答案】(D)
【解析】![]() ,则
,则![]() .
.
(2) 函数![]() 在
在![]() 内( )
内( )
(A) 连续
(B) 有可去间断点
(C) 有跳跃间断点
(D) 有无穷间断点
【答案】(B)
【解析】![]() ,
,![]() ,故
,故![]() 有可去间断点
有可去间断点![]() .
.
(3) 设函数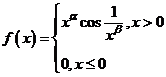
![]() ,若
,若![]() 在
在![]() 处连续则:( )
处连续则:( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
【答案】(A)
【解析】![]() 时,
时,![]()
![]()

![]() 时,
时,![]()
![]()
![]() 在
在![]() 处连续则:
处连续则:![]() 得
得![]()
![]()
得:![]() ,答案选择A
,答案选择A

(4)设函数![]() 在
在![]() 内连续,其中二阶导数
内连续,其中二阶导数![]() 的图形如图所示,则曲线
的图形如图所示,则曲线![]() 的拐点的个数为( )
的拐点的个数为( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
【答案】(C)
【解析】根据图像观察存在两点,二阶导数变号.则拐点个数为2个.
(5) 设函数![]() 满足
满足![]() ,则
,则![]() 与
与![]() 依次是 ( )
依次是 ( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
【答案】(D)
【解析】此题考查二元复合函数偏导的求解.
令![]() ,则
,则![]() ,从而
,从而![]() 变为
变为
![]() .故
.故![]() ,
,
因而![]() .故选(D).
.故选(D).
(6)设![]() 是第一象限由曲线
是第一象限由曲线![]() ,
,![]() 与直线
与直线![]() ,
,![]() 围成的平面区域,函数
围成的平面区域,函数![]() 在
在![]() 上连续,则
上连续,则![]() ( )
( )
(A) ![]()
(B)
(C) ![]()
(D) 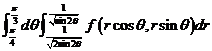
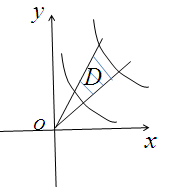
【答案】(B)
【解析】根据图可得,在极坐标系下计算该二重积分的积分区域为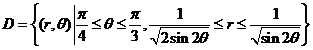
所以

故选B.
(7) 设矩阵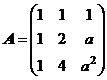 ,
,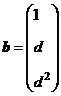 .若集合
.若集合![]() ,则线性方程组
,则线性方程组![]() 有无穷多解的充分必要条件为 ( )
有无穷多解的充分必要条件为 ( )
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
【答案】(D)
【解析】 ,
,
由![]() ,故
,故![]() 或
或![]() ,同时
,同时![]() 或
或![]() .故选(D)
.故选(D)
(8) 设二次型![]() 在正交变换
在正交变换![]() 下的标准形为
下的标准形为![]() ,其中
,其中![]() ,若
,若![]() 则
则![]() 在正交变换
在正交变换![]() 下的标准形为( )
下的标准形为( )
(A)![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
【答案】(A)
【解析】由![]() ,故
,故![]() .
.
且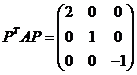 .
.
由已知可得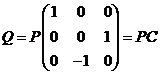
故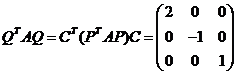
所以![]() .选(A)
.选(A)
二、填空题:9![]() 14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.
14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.
(9) 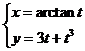 则
则 ![]()
【答案】48
【解析】 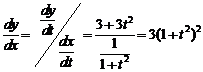
![]()
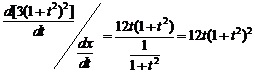
![]() .
.
(10)函数![]() 在
在![]() 处的
处的![]() 阶导数
阶导数![]() _________
_________
【答案】![]()
【解析】根据莱布尼茨公式得:
![]()
(11) 设![]() 连续,
连续,![]() ,若
,若![]() ,则
,则![]()
【答案】![]()
【解析】 已知![]() ,求导得
,求导得![]() ,故有
,故有![]()
![]() 则
则![]() .
.
(12)设函数![]() 是微分方程
是微分方程![]() 的解,且在
的解,且在![]() 处
处![]() 取得极值3,则
取得极值3,则![]() = .
= .
【答案】![]()
【解析】由题意知:![]() ,
,![]() ,由特征方程:
,由特征方程:![]() 解得
解得![]()
所以微分方程的通解为:![]() 代入
代入![]() ,
,![]() 解得:
解得:![]()
![]()
解得:![]()
(13)若函数![]() 由方程
由方程![]() 确定,则
确定,则![]() = .
= .
【答案】![]()
【解析】当![]() 时
时![]() ,则对该式两边求偏导可得
,则对该式两边求偏导可得![]()
![]() .将(0,0,0)点值代入即有
.将(0,0,0)点值代入即有
![]()
则可得![]()
(14) 若![]() 阶矩阵
阶矩阵![]() 的特征值为
的特征值为![]() ,
,![]() ,其中
,其中![]() 为
为![]() 阶单位阵,则行列式
阶单位阵,则行列式![]() .
.
【答案】21
【解析】![]() 的所有特征值为
的所有特征值为![]()
![]() 的所有特征值为
的所有特征值为![]()
所以![]() .
.
三、解答题:15~23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15) (本题满分10分)
设函数![]() ,
,![]() .若
.若![]() 与
与![]() 在
在![]() 时是等价无穷小,求
时是等价无穷小,求![]() 的值.
的值.
【答案】![]()
【解析】
方法一:
因为![]() ,
,![]() ,
,
那么,
 ,
,
可得: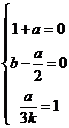 ,所以,
,所以,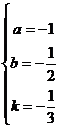 .
.
方法二:
由题意得
![]()
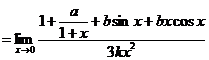
由分母![]() ,得分子
,得分子![]()
![]() ,求得c;
,求得c;
于是![]()
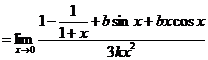
![]()
![]()
![]()
由分母![]() ,得分子
,得分子
![]()
![]() ,
,
求得![]() ;
;
进一步,b值代入原式
![]()
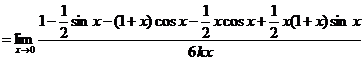
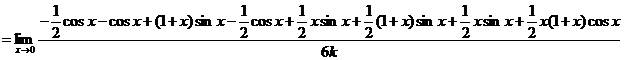
![]() ,求得
,求得![]()
(16) (本题满分10分)
设A>0,D是由曲线段![]() 及直线
及直线![]() ,
,![]() 所围成的平面区域,
所围成的平面区域,![]() ,
,![]() 分别表示D绕
分别表示D绕![]() 轴与绕
轴与绕![]() 轴旋转成旋转体的体积,若
轴旋转成旋转体的体积,若![]() ,求A的值.
,求A的值.
【答案】![]()
【解析】由旋转体的体积公式,得
![]()
![]()
![]()
![]()
![]()
![]()
由题![]() 求得
求得![]()
(17) (本题满分11分)
已知函数![]() 满足
满足![]() ,
,![]() ,
,![]() ,求
,求 ![]() 的极值.
的极值.
【答案】极小值![]()
【解析】![]() 两边对y积分,得
两边对y积分,得
![]()
![]() ,
,
故![]() ,
,
求得![]() ,
,
故![]() ,两边关于x积分,得
,两边关于x积分,得
![]()
![]()
![]()
![]()
![]()
由![]() ,求得
,求得![]()
所以![]() .
.
令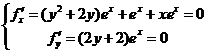 ,求得
,求得![]() .
.
又![]() ,
,
![]() ,
,![]() ,
,
当![]() 时,
时,![]()
![]()
![]() ,
,
![]()
![]() 为极小值.
为极小值.
(18) (本题满分10分)
计算二重积分![]() ,其中
,其中![]()
【答案】![]()
【解析】![]()
![]()
![]()
![]()
![]()
(19)(本题满分 11 分)
已知函数![]() ,求
,求![]() 零点的个数?
零点的个数?
【答案】![]() 个
个
【解析】![]()
令![]() ,得驻点为
,得驻点为![]() ,
,
在![]() ,
,![]() 单调递减,在
单调递减,在![]() ,
,![]() 单调递增
单调递增
故![]() 为唯一的极小值,也是最小值.
为唯一的极小值,也是最小值.
而![]()
![]()
在![]() ,
,![]() ,故
,故![]()
从而有![]()
![]()
![]()
考虑 ,所以
,所以![]() .
.
所以函数![]() 在
在![]() 及
及![]() 上各有一个零点,所以零点个数为2.
上各有一个零点,所以零点个数为2.
(20) (本题满分10分)
已知高温物体置于低温介质中,任一时刻该物体温度对时间的变化率与该时刻物体和介质的温差成正比,现将一初始温度为![]() 的物体在
的物体在![]() 的恒温介质中冷却,30min后该物体降至
的恒温介质中冷却,30min后该物体降至![]() ,若要将该物体的温度继续降至
,若要将该物体的温度继续降至![]() ,还需冷却多长时间?
,还需冷却多长时间?
【答案】![]()
【解析】设![]() 时刻物体温度为
时刻物体温度为![]() ,比例常数为
,比例常数为![]() ,介质温度为
,介质温度为![]() ,则
,则
![]() ,从而
,从而![]() ,
,
![]() ,所以
,所以![]() ,即
,即![]()
又![]() 所以
所以![]() ,所以
,所以![]()
当![]() 时,
时,![]() 1,所以还需要冷却30min.
1,所以还需要冷却30min.
(21) (本题满分10分)
已知函数![]() 在区间
在区间![]() 上具有2阶导数,
上具有2阶导数,![]() ,
,![]() ,
,![]() ,设
,设![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴的交点是
轴的交点是![]() ,证明
,证明![]() .
.
【证明】根据题意得点![]() 处的切线方程为
处的切线方程为![]()
令![]() ,得
,得![]()
因为![]() 所以
所以![]() 单调递增,又因为
单调递增,又因为![]()
所以![]() ,又因为
,又因为![]()
所以![]()
又因为![]() ,而在区间(a,b)上应用拉格朗日中值定理有
,而在区间(a,b)上应用拉格朗日中值定理有
![]()
所以![]()
因为![]() 所以
所以![]() 单调递增
单调递增
所以![]()
所以![]() ,即
,即![]() ,所以
,所以![]() ,结论得证.
,结论得证.
(22) (本题满分 11 分)
设矩阵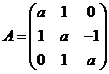 且
且![]() .
.
求![]() 的值;
的值;
若矩阵![]() 满足
满足![]() ,
,![]() 为3阶单位阵,求
为3阶单位阵,求![]() .
.
【答案】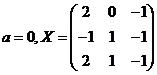
【解析】
(I)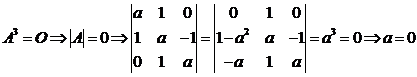
(II)由题意知
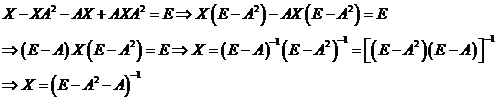
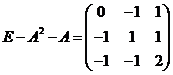 ,
,
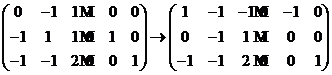

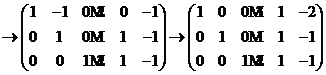
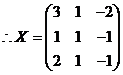
(23) (本题满分11 分)
设矩阵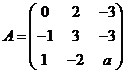 相似于矩阵
相似于矩阵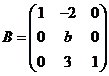 .
.
(1)求![]() 的值;
的值;
(2)求可逆矩阵![]() ,使
,使![]() 为对角阵.
为对角阵.
【答案】
(1)![]() ;
;
(2)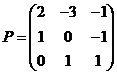
【解析】(I)![]()
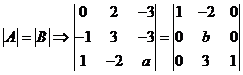
![]()
(II)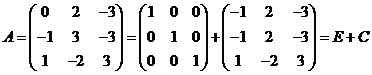
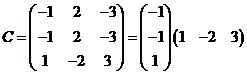
![]() 的特征值
的特征值![]()
![]() 时
时![]() 的基础解系为
的基础解系为![]()
![]() 时
时![]() 的基础解系为
的基础解系为![]()
A的特征值![]()
令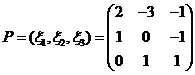 ,
,
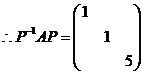
文档内容由金程考研网jjx.gfedu.net 整理发布。
2015年全国硕士研究生入学统一考试数学(一)试题解析
一、选择题:1![]() 8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
(1)设函数![]() 在
在![]() 内连续,其中二阶导数
内连续,其中二阶导数![]() 的图形如图所示,则曲线
的图形如图所示,则曲线![]() 的拐点的个数为 ( )
的拐点的个数为 ( )

(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
【答案】(C)
【解析】拐点出现在二阶导数等于0,或二阶导数不存在的点,并且在这点的左右两侧二阶导函数异号.因此,由![]() 的图形可得,曲线
的图形可得,曲线![]() 存在两个拐点.故选(C).
存在两个拐点.故选(C).
(2)设![]() 是二阶常系数非齐次线性微分方程
是二阶常系数非齐次线性微分方程![]() 的一个特解,则( )
的一个特解,则( )
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
【答案】(A)
【分析】此题考查二阶常系数非齐次线性微分方程的反问题——已知解来确定微分方程的系数,此类题有两种解法,一种是将特解代入原方程,然后比较等式两边的系数可得待估系数值,另一种是根据二阶线性微分方程解的性质和结构来求解,也就是下面演示的解法.
【解析】由题意可知,![]() 、
、![]() 为二阶常系数齐次微分方程
为二阶常系数齐次微分方程![]() 的解,所以2,1为特征方程
的解,所以2,1为特征方程![]() 的根,从而
的根,从而![]() ,
,![]() ,从而原方程变为
,从而原方程变为![]() ,再将特解
,再将特解![]() 代入得
代入得![]() .故选(A)
.故选(A)
(3) 若级数![]() 条件收敛,则
条件收敛,则 ![]() 与
与![]() 依次为幂级数
依次为幂级数![]() 的 ( )
的 ( )
(A) 收敛点,收敛点
(B) 收敛点,发散点
(C) 发散点,收敛点
(D) 发散点,发散点
【答案】(B)
【分析】此题考查幂级数收敛半径、收敛区间,幂级数的性质.
【解析】因为![]() 条件收敛,即
条件收敛,即![]() 为幂级数
为幂级数![]() 的条件收敛点,所以
的条件收敛点,所以![]() 的收敛半径为1,收敛区间为
的收敛半径为1,收敛区间为![]() .而幂级数逐项求导不改变收敛区间,故
.而幂级数逐项求导不改变收敛区间,故![]() 的收敛区间还是
的收敛区间还是![]() .因而
.因而![]() 与
与![]() 依次为幂级数
依次为幂级数![]() 的收敛点,发散点.故选(B).
的收敛点,发散点.故选(B).
(4) 设![]() 是第一象限由曲线
是第一象限由曲线![]() ,
,![]() 与直线
与直线![]() ,
,![]() 围成的平面区域,函数
围成的平面区域,函数![]() 在
在![]() 上连续,则
上连续,则![]() ( )
( )
(A) ![]()
(B)
(C) ![]()
(D) 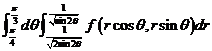
![]()
![]()
![]()
【答案】(B)
【分析】此题考查将二重积分化成极坐标系下的累次积分
【解析】先画出D的图形,
所以![]()
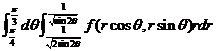 ,
,
故选(B)
(5) 设矩阵 ,
, ,若集合
,若集合![]() ,则线性方程组
,则线性方程组![]() 有无穷多解的充分必要条件为 ( )
有无穷多解的充分必要条件为 ( )
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
【答案】(D)
【解析】 ,
,
由![]() ,故
,故![]() 或
或![]() ,同时
,同时![]() 或
或![]() .故选(D)
.故选(D)
(6)设二次型![]() 在正交变换为
在正交变换为![]() 下的标准形为
下的标准形为![]() ,其中
,其中![]() ,若
,若![]() ,则
,则![]() 在正交变换
在正交变换![]() 下的标准形为( )
下的标准形为( )
(A) ![]()
(B) ![]()
(C) ![]()
(D) ![]()
【答案】(A)
【解析】由![]() ,故
,故![]() .
.
且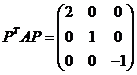 .
.
由已知可得: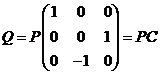
故有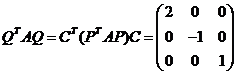
所以![]() .选(A)
.选(A)
(7) 若A,B为任意两个随机事件,则 ( )
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
【答案】(C)
【解析】由于![]() ,按概率的基本性质,我们有
,按概率的基本性质,我们有![]() 且
且![]() ,从而
,从而![]() ,选(C) .
,选(C) .
(8)设随机变量![]() 不相关,且
不相关,且![]() ,则
,则![]() ( )
( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
【答案】(D)
【解析】![]()
![]()
![]() ,选(D) .
,选(D) .
二、填空题:9![]() 14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.
14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.
(9) ![]()
【答案】![]()
【分析】此题考查![]() 型未定式极限,可直接用洛必达法则,也可以用等价无穷小替换.
型未定式极限,可直接用洛必达法则,也可以用等价无穷小替换.
【解析】方法一: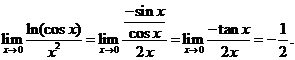
方法二: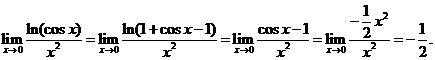
(10) ![]()
【答案】![]()
【分析】此题考查定积分的计算,需要用奇偶函数在对称区间上的性质化简.
【解析】![]()
(11)若函数![]() 由方程
由方程![]() 确定,则
确定,则![]()
【答案】![]()
【分析】此题考查隐函数求导.
【解析】令![]() ,则
,则
![]()
又当![]() 时
时![]() ,即
,即![]() .
.
所以![]() ,因而
,因而![]()
(12)设![]() 是由平面
是由平面![]() 与三个坐标平面平面所围成的空间区域,则
与三个坐标平面平面所围成的空间区域,则![]()
【答案】![]()
【分析】此题考查三重积分的计算,可直接计算,也可以利用轮换对称性化简后再计算.
【解析】由轮换对称性,得
![]() ,
,
其中![]() 为平面
为平面![]() 截空间区域
截空间区域![]() 所得的截面,其面积为
所得的截面,其面积为![]() .所以
.所以
![]() (13)
(13) ![]() 阶行列式
阶行列式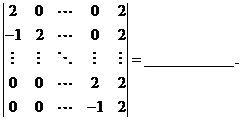
【答案】![]()
【解析】按第一行展开得
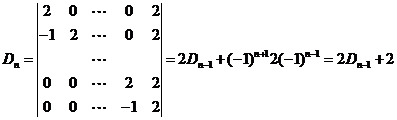
![]()
![]()
(14)设二维随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]()
【答案】 ![]()
【解析】由题设知,![]() ,而且
,而且![]() 相互独立,从而
相互独立,从而
![]()
![]() .
.
三、解答题:15~23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分10分) 设函数![]() ,
,![]() ,若
,若![]() 与
与![]() 在
在![]() 是等价无穷小,求
是等价无穷小,求![]() 的值.
的值.
【答案】![]()
【解析】法一:原式![]()
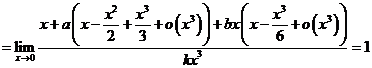
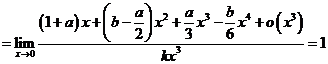
即![]()
![]()
法二:![]()
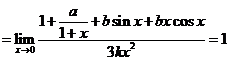
因为分子的极限为0,则![]()
 ,分子的极限为0,
,分子的极限为0,![]()
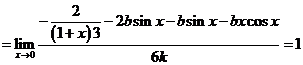 ,
,![]()
![]()
(16)(本题满分10分) 设函数![]() 在定义域I上的导数大于零,若对任意的
在定义域I上的导数大于零,若对任意的![]() ,由线
,由线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 及
及![]() 轴所围成区域的面积恒为4,且
轴所围成区域的面积恒为4,且![]() ,求
,求![]() 的表达式.
的表达式.
【答案】![]() .
.
【解析】设![]() 在点
在点![]() 处的切线方程为:
处的切线方程为:![]()
令![]() ,得到
,得到![]() ,
,
故由题意,![]() ,即
,即![]() ,可以转化为一阶微分方程,
,可以转化为一阶微分方程,
即![]() ,可分离变量得到通解为:
,可分离变量得到通解为:![]() ,
,
已知![]() ,得到
,得到![]() ,因此
,因此![]() ;
;
即![]() .
.
(17)(本题满分10分)
已知函数![]() ,曲线C:
,曲线C:![]() ,求
,求![]() 在曲线C上的最大方向导数.
在曲线C上的最大方向导数.
【答案】3
【解析】因为![]() 沿着梯度的方向的方向导数最大,且最大值为梯度的模.
沿着梯度的方向的方向导数最大,且最大值为梯度的模.
![]() ,
,
故![]() ,模为
,模为![]() ,
,
此题目转化为对函数![]() 在约束条件
在约束条件![]() 下的最大值.即为条件极值问题.
下的最大值.即为条件极值问题.
为了计算简单,可以转化为对![]() 在约束条件
在约束条件![]() 下的最大值.
下的最大值.
构造函数:![]()
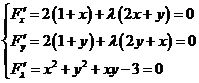 ,得到
,得到![]() .
.
![]()
所以最大值为![]() .
.
(18)(本题满分 10 分)
(I)设函数![]() 可导,利用导数定义证明
可导,利用导数定义证明![]()
(II)设函数![]() 可导,
可导,![]() ,写出
,写出![]() 的求导公式.
的求导公式.
【解析】(I)![]()
![]()
![]()
![]()
(II)由题意得
![]()
![]()
(19)(本题满分 10 分)
已知曲线L的方程为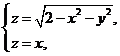 起点为
起点为![]() ,终点为
,终点为![]() ,计算曲线积分
,计算曲线积分![]() .
.
【答案】![]()
【解析】由题意假设参数方程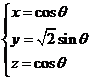 ,
,![]()
![]()
![]()
![]()
(20) (本题满11分)
设向量组![]() 内
内![]() 的一个基,
的一个基,![]() ,
,![]() ,
,![]() .
.
(I)证明向量组![]()
![]()
![]() 为
为![]() 的一个基;
的一个基;
(II)当k为何值时,存在非0向量![]() 在基
在基![]() 与基
与基![]()
![]()
![]() 下的坐标相同,并求所有的
下的坐标相同,并求所有的![]() .
.
【答案】
【解析】(I)证明:

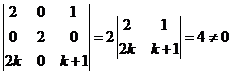
故![]() 为
为![]() 的一个基.
的一个基.
(II)由题意知,![]()
即![]()
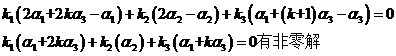
即![]()
即 ,得k=0
,得k=0
![]()
![]()
(21) (本题满分11 分)
设矩阵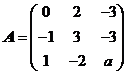 相似于矩阵
相似于矩阵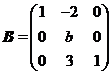 .
.
求![]() 的值;
的值;
(II)求可逆矩阵![]() ,使
,使![]() 为对角矩阵..
为对角矩阵..
【解析】(I) ![]()
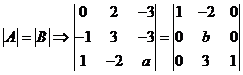
![]()
(II)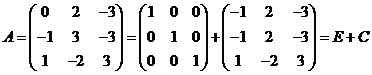
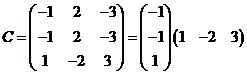
![]() 的特征值
的特征值![]()
![]() 时
时![]() 的基础解系为
的基础解系为![]()
![]() 时
时![]() 的基础解系为
的基础解系为![]()
A的特征值![]()
令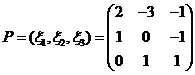 ,
,
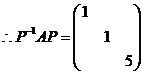
(22) (本题满分11 分) 设随机变量![]() 的概率密度为
的概率密度为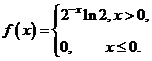
对![]() 进行独立重复的观测,直到2个大于3的观测值出现的停止.记
进行独立重复的观测,直到2个大于3的观测值出现的停止.记![]() 为观测次数.
为观测次数.
(I)求![]() 的概率分布;
的概率分布;
(II)求![]()
【解析】(I) 记![]() 为观测值大于3的概率,则
为观测值大于3的概率,则![]() ,
,
从而![]() ,
,![]()
为![]() 的概率分布;
的概率分布;
(II) 法一:分解法:
将随机变量![]() 分解成
分解成![]() 两个过程,其中
两个过程,其中![]() 表示从
表示从![]() 到
到![]() 次试验观测值大于
次试验观测值大于![]() 首次发生,
首次发生,![]() 表示从
表示从![]() 次到第
次到第![]() 试验观测值大于
试验观测值大于![]() 首次发生.
首次发生.
则![]() ,
,![]() (注:Ge表示几何分布)
(注:Ge表示几何分布)
所以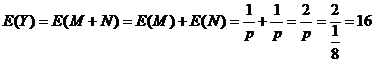 .
.
法二:直接计算
![]() 记
记![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
所以![]() ,
,
从而![]() .
.
(23) (本题满分 11 分)设总体X的概率密度为:
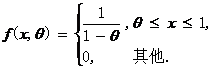
其中![]() 为未知参数,
为未知参数,![]() 为来自该总体的简单随机样本.
为来自该总体的简单随机样本.
(I)求![]() 的矩估计量.
的矩估计量.
(II)求![]() 的最大似然估计量.
的最大似然估计量.
【解析】(I) ![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() 为
为![]() 的矩估计量;
的矩估计量;
(II) 似然函数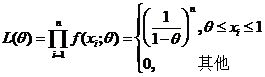 ,
,
当![]() 时,
时,![]() ,则
,则![]() .
.
从而![]() ,关于
,关于![]() 单调增加,
单调增加,
所以![]() 为
为![]() 的最大似然估计量.
的最大似然估计量.
文档内容由经济学金融硕士考研金程考研网jjx.gfedu.net 整理发布。
2014年考研数学二真题与解析
1.当![]() 时,若
时,若![]() ,
,![]() 均是比
均是比![]() 高阶的无穷小,则
高阶的无穷小,则![]() 的可能取值范围是( )
的可能取值范围是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
【详解】![]() ,是
,是![]() 阶无穷小,
阶无穷小,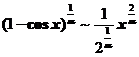 是
是![]() 阶无穷小,由题意可知
阶无穷小,由题意可知![]()
所以![]() 的可能取值范围是
的可能取值范围是![]() ,应该选(B).
,应该选(B).
2.下列曲线有渐近线的是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
【详解】对于![]() ,可知
,可知![]() 且
且![]() ,所以有斜渐近线
,所以有斜渐近线![]()
应该选(C)
3.设函数![]() 具有二阶导数,
具有二阶导数,![]() ,则在
,则在![]() 上( )
上( )
(A)当![]() 时,
时,![]() (B)当
(B)当![]() 时,
时,![]()
(C)当![]() 时,
时,![]() (D)当
(D)当![]() 时,
时,![]()
【分析】此题考查的曲线的凹凸性的定义及判断方法.
【详解1】如果对曲线在区间![]() 上凹凸的定义比较熟悉的话,可以直接做出判断. 显然
上凹凸的定义比较熟悉的话,可以直接做出判断. 显然![]() 就是联接
就是联接![]() 两点的直线方程.故当
两点的直线方程.故当![]() 时,曲线是凹的,也就是
时,曲线是凹的,也就是![]() ,应该选(D)
,应该选(D)
【详解2】如果对曲线在区间![]() 上凹凸的定义不熟悉的话,可令
上凹凸的定义不熟悉的话,可令![]() ,则
,则![]() ,且
,且![]() ,故当
,故当![]() 时,曲线是凹的,从而
时,曲线是凹的,从而![]() ,即
,即![]() ,也就是
,也就是![]() ,应该选(D)
,应该选(D)
4.曲线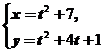 上对应于
上对应于![]() 的点处的曲率半径是( )
的点处的曲率半径是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
【详解】 曲线在点![]() 处的曲率公式
处的曲率公式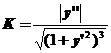 ,曲率半径
,曲率半径![]() .
.
本题中![]() ,所以
,所以![]() ,
, ,
,
对应于![]() 的点处
的点处![]() ,所以
,所以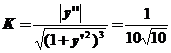 ,曲率半径
,曲率半径![]() .
.
应该选(C)
5.设函数![]() ,若
,若![]() ,则
,则![]() ( )
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
【详解】注意(1)![]() ,(2)
,(2)![]() .
.
由于![]() .所以可知
.所以可知![]() ,
,![]() ,
,
 .
.
6.设![]() 在平面有界闭区域D上连续,在D的内部具有二阶连续偏导数,且满足
在平面有界闭区域D上连续,在D的内部具有二阶连续偏导数,且满足![]() 及
及![]() ,则( ).
,则( ).
(A)![]() 的最大值点和最小值点必定都在区域D的边界上;
的最大值点和最小值点必定都在区域D的边界上;
(B)![]() 的最大值点和最小值点必定都在区域D的内部;
的最大值点和最小值点必定都在区域D的内部;
(C)![]() 的最大值点在区域D的内部,最小值点在区域D的边界上;
的最大值点在区域D的内部,最小值点在区域D的边界上;
(D)![]() 的最小值点在区域D的内部,最大值点在区域D的边界上.
的最小值点在区域D的内部,最大值点在区域D的边界上.
【详解】![]() 在平面有界闭区域D上连续,所以
在平面有界闭区域D上连续,所以![]() 在D内必然有最大值和最小值.并且如果在内部存在驻点
在D内必然有最大值和最小值.并且如果在内部存在驻点![]() ,也就是
,也就是![]() ,在这个点处
,在这个点处![]() ,由条件,显然
,由条件,显然![]() ,显然
,显然![]() 不是极值点,当然也不是最值点,所以
不是极值点,当然也不是最值点,所以![]() 的最大值点和最小值点必定都在区域D的边界上.
的最大值点和最小值点必定都在区域D的边界上.
所以应该选(A).
7.行列式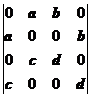 等于
等于
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
【详解】
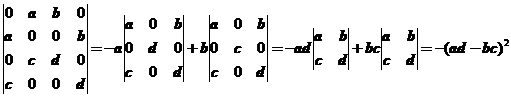
应该选(B).
8.设![]() 是三维向量,则对任意的常数
是三维向量,则对任意的常数![]() ,向量
,向量![]() ,
,![]() 线性无关是向量
线性无关是向量![]() 线性无关的
线性无关的
(A)必要而非充分条件 (B)充分而非必要条件
(C)充分必要条件 (D) 非充分非必要条件
【详解】若向量![]() 线性无关,则
线性无关,则
(![]() ,
,![]() )
)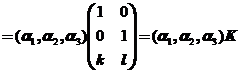 ,对任意的常数
,对任意的常数![]() ,矩阵
,矩阵![]() 的秩都等于2,所以向量
的秩都等于2,所以向量![]() ,
,![]() 一定线性无关.
一定线性无关.
而当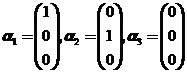 时,对任意的常数
时,对任意的常数![]() ,向量
,向量![]() ,
,![]() 线性无关,但
线性无关,但![]() 线性相关;故选择(A).
线性相关;故选择(A).
9.![]() .
.
【详解】![]() .
.
10.设![]() 为周期为4的可导奇函数,且
为周期为4的可导奇函数,且![]() ,则
,则![]() .
.
【详解】当![]() 时,
时,![]() ,由
,由![]() 可知
可知![]() ,即
,即![]() ;
;![]() 为周期为4奇函数,故
为周期为4奇函数,故![]() .
.
11.设![]() 是由方程
是由方程![]() 确定的函数,则
确定的函数,则![]() .
.
【详解】设![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,
,![]() ,所以
,所以![]()
![]() .
.
12.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,则
,则![]() 在点
在点![]() 处的切线方程为 .
处的切线方程为 .
【详解】先把曲线方程化为参数方程![]() ,于是在
,于是在![]() 处,
处,![]() ,
,![]() ,则
,则![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]()
13.一根长为1的细棒位于![]() 轴的区间
轴的区间![]() 上,若其线密度
上,若其线密度![]() ,则该细棒的质心坐标
,则该细棒的质心坐标![]() .
.
【详解】质心坐标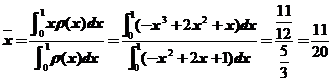 .
.
14.设二次型![]() 的负惯性指数是1,则
的负惯性指数是1,则![]() 的取值范围是 .
的取值范围是 .
【详解】由配方法可知
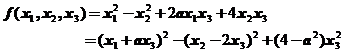
由于负惯性指数为1,故必须要求![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.
15.(本题满分10分)
求极限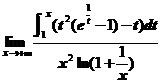 .
.
【分析】.先用等价无穷小代换简化分母,然后利用洛必达法则求未定型极限.
【详解】

16.(本题满分10分)
已知函数![]() 满足微分方程
满足微分方程![]() ,且
,且![]() ,求
,求![]() 的极大值和极小值.
的极大值和极小值.
【详解】
解:把方程化为标准形式得到![]() ,这是一个可分离变量的一阶微分方程,两边分别积分可得方程通解为:
,这是一个可分离变量的一阶微分方程,两边分别积分可得方程通解为:![]() ,由
,由![]() 得
得![]() ,
,
即![]() .
.
令![]() ,得
,得![]() ,且可知
,且可知![]() ;
;
当![]() 时,可解得
时,可解得![]() ,
,![]() ,函数取得极大值
,函数取得极大值![]() ;
;
当![]() 时,可解得
时,可解得![]() ,
,![]() ,函数取得极小值
,函数取得极小值![]() .
.
17.(本题满分10分)
设平面区域![]() .计算
.计算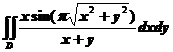
【详解】由对称性可得
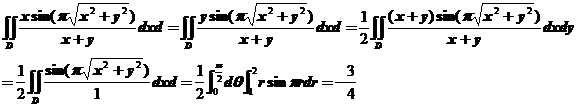
18.(本题满分10分)
设函数![]() 具有二阶连续导数,
具有二阶连续导数,![]() 满足
满足![]() .若
.若![]() ,求
,求![]() 的表达式.
的表达式.
【详解】
设![]() ,则
,则![]() ,
,
![]() ;
;
![]() ;
;
![]()
由条件![]() ,
,
可知
![]()
这是一个二阶常用系数线性非齐次方程.
对应齐次方程的通解为:
![]() 其中
其中![]() 为任意常数.
为任意常数.
对应非齐次方程特解可求得为![]() .
.
故非齐次方程通解为![]() .
.
将初始条件![]() 代入,可得
代入,可得![]() .
.
所以![]() 的表达式为
的表达式为![]() .
.
19.(本题满分10分)
设函数![]() 在区间
在区间![]() 上连续,且
上连续,且![]() 单调增加,
单调增加,![]() ,证明:
,证明:
![]() ;
;
![]() .
.
【详解】
(1)证明:因为![]() ,所以
,所以![]() .
.
即![]() .
.
(2)令![]() ,
,
则可知![]() ,且
,且![]() ,
,
因为![]() 且
且![]() 单调增加,
单调增加,
所以![]() .从而
.从而
![]() ,
, ![]()
也是![]() 在
在![]() 单调增加,则
单调增加,则![]() ,即得到
,即得到
![]() .
.
20.(本题满分11分)
设函数![]() ,定义函数列
,定义函数列
![]() ,
,![]() ,
,![]()
设![]() 是曲线
是曲线![]() ,直线
,直线![]() 所围图形的面积.求极限
所围图形的面积.求极限![]() .
.
【详解】
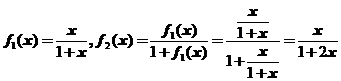 ,
,![]() ,
,
利用数学归纳法可得![]()
![]() ,
,
![]() .
.
21.(本题满分11分)
已知函数![]() 满足
满足![]() ,且
,且![]() ,求曲线
,求曲线![]() 所成的图形绕直线
所成的图形绕直线![]() 旋转所成的旋转体的体积.
旋转所成的旋转体的体积.
【详解】
由于函数![]() 满足
满足![]() ,所以
,所以![]() ,其中
,其中![]() 为待定的连续函数.
为待定的连续函数.
又因为![]() ,从而可知
,从而可知![]() ,
,
得到![]() .
.
令![]() ,可得
,可得![]() .且当
.且当![]() 时,
时,![]() .
.
曲线![]() 所成的图形绕直线
所成的图形绕直线![]() 旋转所成的旋转体的体积为
旋转所成的旋转体的体积为
![]()
22.(本题满分11分)
设 ,E为三阶单位矩阵.
,E为三阶单位矩阵.
求方程组![]() 的一个基础解系;
的一个基础解系;
求满足![]() 的所有矩阵.
的所有矩阵.
【详解】(1)对系数矩阵A进行初等行变换如下:
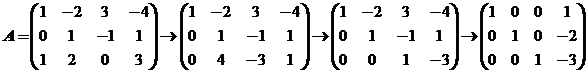 ,
,
得到方程组![]() 同解方程组
同解方程组
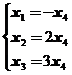
得到![]() 的一个基础解系
的一个基础解系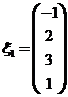 .
.
(2)显然B矩阵是一个![]() 矩阵,设
矩阵,设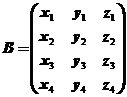
对矩阵![]() 进行进行初等行变换如下:
进行进行初等行变换如下:
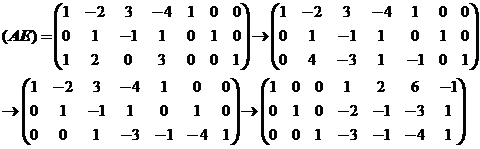
由方程组可得矩阵B对应的三列分别为
 ,
,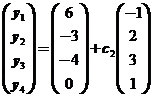 ,
,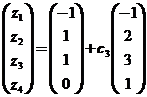 ,
,
即满足![]() 的所有矩阵为
的所有矩阵为
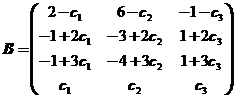
其中![]() 为任意常数.
为任意常数.
23.(本题满分11分)
证明![]() 阶矩阵
阶矩阵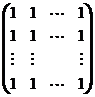 与
与 相似.
相似.
【详解】证明:设![]()
 ,
,![]()
 .
.
分别求两个矩阵的特征值和特征向量如下:
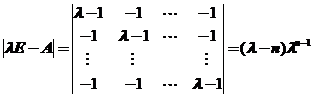 ,
,
所以A的![]() 个特征值为
个特征值为![]() ;
;
而且A是实对称矩阵,所以一定可以对角化.且 ;
;
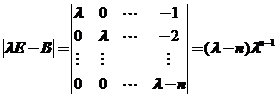
所以B的![]() 个特征值也为
个特征值也为![]() ;
;
对于![]() 重特征值
重特征值![]() ,由于矩阵
,由于矩阵![]() 的秩显然为1,所以矩阵B对应
的秩显然为1,所以矩阵B对应![]() 重特征值
重特征值![]() 的特征向量应该有
的特征向量应该有![]() 个线性无关,进一步矩阵B存在
个线性无关,进一步矩阵B存在![]() 个线性无关的特征向量,即矩阵B一定可以对角化,且
个线性无关的特征向量,即矩阵B一定可以对角化,且
从而可知![]() 阶矩阵
阶矩阵 与
与 相似.
相似.
2013年考研数学二真题及答案





数学二答案:

![]()




一、选择题:1-8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
(1)曲线![]() 的渐近线条数 ( )
的渐近线条数 ( )
(A) 0 (B) 1 (C) 2 (D) 3
(2) 设函数![]() ,其中
,其中![]() 为正整数,则
为正整数,则![]() ( )
( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(3) 设![]() ,则数列
,则数列![]() 有界是数列
有界是数列![]() 收敛的
收敛的
( )
(A) 充分必要条件 (B) 充分非必要条件
(C) 必要非充分条件 (D) 非充分也非必要
(4) 设![]() 则有
则有
( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(5) 设函数![]() 为可微函数,且对任意的
为可微函数,且对任意的![]() 都有
都有![]() 则使不等式
则使不等式![]() 成立的一个充分条件是
成立的一个充分条件是
( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(6) 设区域![]() 由曲线
由曲线![]() 围成,则
围成,则![]()
( )
(A) ![]() (B) 2 (C) -2 (D) -
(B) 2 (C) -2 (D) -![]()
(7) 设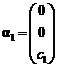 ,
,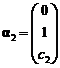 ,
,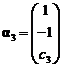 ,
,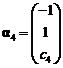 ,其中
,其中![]() 为任意常数,则下列向量组线性相关的为 ( )
为任意常数,则下列向量组线性相关的为 ( )
(A)![]() (B)
(B) ![]() (C)
(C)![]() (D)
(D)![]()
(8) 设![]() 为3阶矩阵,
为3阶矩阵,![]() 为3阶可逆矩阵,且
为3阶可逆矩阵,且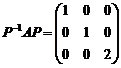 .若
.若![]() ,
,![]() 则
则![]() ( )
( )
(A) 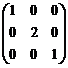 (B)
(B) 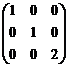 (C)
(C) 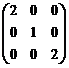 (D)
(D)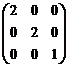
二、填空题:9-14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.
(9) 设![]() 是由方程
是由方程![]() 所确定的隐函数,则
所确定的隐函数,则![]() .
.
(10) ![]() .
.
(11) 设![]() 其中函数
其中函数![]() 可微,则
可微,则![]() .
.
(12) 微分方程![]() 满足条件
满足条件![]() 的解为
的解为![]() .
.
(13) 曲线![]() 上曲率为
上曲率为![]() 的点的坐标是 .
的点的坐标是 .
(14) 设![]() 为3阶矩阵,
为3阶矩阵,![]() ,
,![]() 为
为![]() 伴随矩阵,若交换
伴随矩阵,若交换![]() 的第1行与第2行得矩阵
的第1行与第2行得矩阵![]() ,则
,则![]() .
.
三、解答题:15-23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分 10 分)
已知函数![]() ,记
,记![]() ,
,
(I)求![]() 的值;
的值;
(II)若![]() 时,
时,![]() 与
与![]() 是同阶无穷小,求常数
是同阶无穷小,求常数![]() 的值.
的值.
(16)(本题满分 10 分)
求函数![]() 的极值.
的极值.
(17)(本题满分12分)
过![]() 点作曲线
点作曲线![]() 的切线,切点为
的切线,切点为![]() ,又
,又![]() 与
与![]() 轴交于
轴交于![]() 点,区域
点,区域![]() 由
由![]() 与直线
与直线![]() 围成,求区域
围成,求区域![]() 的面积及
的面积及![]() 绕
绕![]() 轴旋转一周所得旋转体的体积.
轴旋转一周所得旋转体的体积.
(18)(本题满分 10 分)
计算二重积分![]() ,其中区域
,其中区域![]() 为曲线
为曲线![]() 与极轴围成.
与极轴围成.
(19)(本题满分10分)
已知函数![]() 满足方程
满足方程![]() 及
及![]() ,
,
(I) 求![]() 的表达式;
的表达式;
(II) 求曲线![]() 的拐点.
的拐点.
(20)(本题满分10分)
证明![]() ,
,![]() .
.
(21)(本题满分10 分)
(I)证明方程![]()
![]() ,在区间
,在区间![]() 内有且仅有一个实根;
内有且仅有一个实根;
(II)记(I)中的实根为![]() ,证明
,证明![]() 存在,并求此极限.
存在,并求此极限.
(22)(本题满分11 分)
设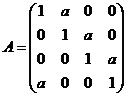 ,
,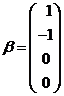
(I) 计算行列式![]() ;
;
(II) 当实数![]() 为何值时,方程组
为何值时,方程组![]() 有无穷多解,并求其通解.
有无穷多解,并求其通解.
(23)(本题满分11 分)
已知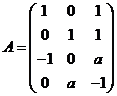 ,二次型
,二次型![]() 的秩为2,
的秩为2,
(I) 求实数![]() 的值;
的值;
(II) 求正交变换![]() 将
将![]() 化为标准形.
化为标准形.






2010年考研数学二真题
一 填空题(8×4=32分)





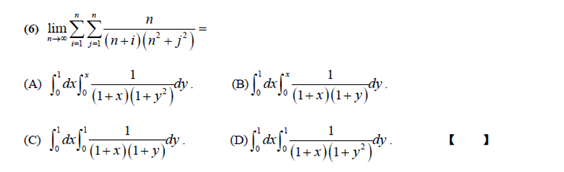




![]()
![]()
![]()
![]()





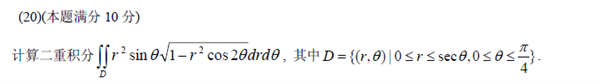



2009年全国硕士研究生入学统一考试
数学二试题
一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.
(1)函数![]() 的可去间断点的个数,则( )
的可去间断点的个数,则( )
![]() 1.
1. ![]() 2.
2. ![]() 3.
3. ![]() 无穷多个.
无穷多个.
(2)当![]() 时,
时,![]() 与
与![]() 是等价无穷小,则( )
是等价无穷小,则( )
![]()
![]() .
. ![]()
![]() .
. ![]()
![]() .
. ![]()
![]() .
.
(3)设函数![]() 的全微分为
的全微分为![]() ,则点
,则点![]() ( )
( )
![]() 不是
不是![]() 的连续点.
的连续点. ![]() 不是
不是![]() 的极值点.
的极值点.
![]() 是
是![]() 的极大值点.
的极大值点. ![]() 是
是![]() 的极小值点.
的极小值点.
(4)设函数![]() 连续,则
连续,则![]() ( )
( )
![]()
![]() .
. ![]()
![]() .
.
![]()
![]() .
. ![]() .
.![]()
(5)若![]() 不变号,且曲线
不变号,且曲线![]() 在点
在点![]() 上的曲率圆为
上的曲率圆为![]() ,则
,则![]() 在区间
在区间![]() 内( )
内( )
![]() 有极值点,无零点.
有极值点,无零点. ![]() 无极值点,有零点.
无极值点,有零点.
![]() 有极值点,有零点.
有极值点,有零点. ![]() 无极值点,无零点.
无极值点,无零点.
(6)设函数![]() 在区间
在区间![]() 上的图形为:
上的图形为:
1
![]()
-2
0
2
3
![]()
-1
O
则函数![]() 的图形为( )
的图形为( )
![]() .
.
![]()
0
2
3
![]()
1
-2
-1
1
![]()
0
2
3
![]()
1
-2
-1
1
![]() .
.
![]()
0
2
3
![]()
1
-1
1
![]()
0
2
3
![]()
1
-2
-1
1
(7)设![]() 、
、![]() 均为2阶矩阵,
均为2阶矩阵,![]() 分别为
分别为![]() 、
、![]() 的伴随矩阵。若
的伴随矩阵。若![]() ,则分块矩阵
,则分块矩阵![]() 的伴随矩阵为( )
的伴随矩阵为( )
![]() .
.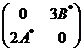
![]() .
.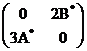
![]() .
.
![]() .
.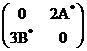
(8)设![]() 均为3阶矩阵,
均为3阶矩阵,![]() 为
为![]() 的转置矩阵,且
的转置矩阵,且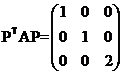 ,若
,若
![]() ,则
,则![]() 为( )
为( )
![]() .
.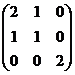
![]() .
.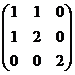
![]() .
.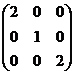
![]() .
.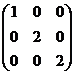
二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.
(9)曲线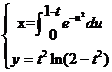 在
在![]() 处的切线方程为
处的切线方程为
(10)已知![]() ,则
,则![]()
(11)![]()
(12)设![]() 是由方程
是由方程![]() 确定的隐函数,则
确定的隐函数,则![]()
(13)函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为
(14)设![]() 为3维列向量,
为3维列向量,![]() 为
为![]() 的转置,若矩阵
的转置,若矩阵![]() 相似于
相似于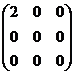 ,则
,则![]()
三、解答题:15-23小题,共94分.请将解答写在答题纸指定的位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分9分)求极限![]()
(16)(本题满分10 分)计算不定积分![]()
![]()
(17)(本题满分10分)设![]() ,其中
,其中![]() 具有2阶连续偏导数,求
具有2阶连续偏导数,求![]() 与
与![]()
(18)(本题满分10分)
设非负函数![]()
![]() 满足微分方程
满足微分方程![]() ,当曲线
,当曲线![]() 过原点时,其与直线
过原点时,其与直线![]() 及
及![]() 围成平面区域
围成平面区域![]() 的面积为2,求
的面积为2,求![]() 绕
绕![]() 轴旋转所得旋转体体积。
轴旋转所得旋转体体积。
(19)(本题满分10分)求二重积分![]() ,
,
其中![]()
(20)(本题满分12分)
设![]() 是区间
是区间![]() 内过
内过![]() 的光滑曲线,当
的光滑曲线,当![]() 时,曲线上任一点处的法线都过原点,当
时,曲线上任一点处的法线都过原点,当![]() 时,函数
时,函数![]() 满足
满足![]() 。求
。求![]() 的表达式
的表达式
(21)(本题满分11分)
(Ⅰ)证明拉格朗日中值定理:若函数![]() 在
在![]() 上连续,在
上连续,在![]() 可导,则存在
可导,则存在![]() ,使得
,使得![]() (Ⅱ)证明:若函数
(Ⅱ)证明:若函数![]() 在
在![]() 处连续,在
处连续,在![]() 内可导,且
内可导,且![]() ,则
,则![]() 存在,且
存在,且![]() 。
。
(22)(本题满分11分)设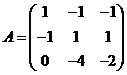 ,
,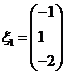
(Ⅰ)求满足![]() 的所有向量
的所有向量![]()
(Ⅱ)对(Ⅰ)中的任一向量![]() ,证明:
,证明:![]() 线性无关。
线性无关。
(23)(本题满分11分)设二次型![]()
(Ⅰ)求二次型![]() 的矩阵的所有特征值;
的矩阵的所有特征值;
(Ⅱ)若二次型![]() 的规范形为
的规范形为![]() ,求
,求![]() 的值。
的值。
2008年全国硕士研究生入学统一考试
数学二试题
一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.
(1)设![]() ,则
,则![]() 的零点个数为( )
的零点个数为( )
![]() 0
0 ![]() 1.
1. ![]() 2
2 ![]() 3
3
(2)曲线方程为![]() 函数在区间
函数在区间![]() 上有连续导数,则定积分
上有连续导数,则定积分![]() ( )
( )
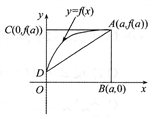
![]() 曲边梯形ABOD面积.
曲边梯形ABOD面积.
![]() 梯形ABOD面积.
梯形ABOD面积.
![]() 曲边三角形
曲边三角形![]() 面积.
面积.
![]() 三角形
三角形![]() 面积.
面积.
(3)在下列微分方程中,以![]() (
(![]() 为任意常数)为通解的是( )
为任意常数)为通解的是( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(5)设函数![]() 在
在![]() 内单调有界,
内单调有界,![]() 为数列,下列命题正确的是( )
为数列,下列命题正确的是( )
![]() 若
若![]() 收敛,则
收敛,则![]() 收敛.
收敛. ![]() 若
若![]() 单调,则
单调,则![]() 收敛.
收敛.
![]() 若
若![]() 收敛,则
收敛,则![]() 收敛.
收敛. ![]() 若
若![]() 单调,则
单调,则![]() 收敛.
收敛.
(6)设函数![]() 连续,若
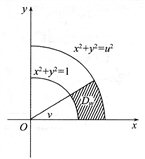
连续,若 ,其中区域
,其中区域![]() 为图中阴影部分,则
为图中阴影部分,则![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(7)设![]() 为
为![]() 阶非零矩阵,
阶非零矩阵,![]() 为
为![]() 阶单位矩阵. 若
阶单位矩阵. 若![]() ,则( )
,则( )
![]()
![]() 不可逆,
不可逆,![]() 不可逆.
不可逆. ![]()
![]() 不可逆,
不可逆,![]() 可逆.
可逆.
![]()
![]() 可逆,
可逆,![]() 可逆.
可逆. ![]()
![]() 可逆,
可逆,![]() 不可逆.
不可逆.
(8)设![]() ,则在实数域上与
,则在实数域上与![]() 合同的矩阵为( )
合同的矩阵为( )
![]()
![]() .
. ![]()
![]() .
.
![]()
![]() .
. ![]()
![]() .
.
二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.
(9) 已知函数![]() 连续,且
连续,且![]() ,则
,则![]() .
.
(10)微分方程![]() 的通解是
的通解是![]() .
.
(11)曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(12)曲线![]() 的拐点坐标为______.
的拐点坐标为______.
(13)设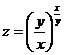 ,则
,则![]() .
.
(14)设3阶矩阵![]() 的特征值为
的特征值为![]() .若行列式
.若行列式![]() ,则
,则![]() .
.
三、解答题:15-23题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分9分)求极限![]() .
.
(16)(本题满分10分)
设函数![]() 由参数方程
由参数方程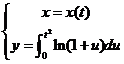 确定,其中
确定,其中![]() 是初值问题
是初值问题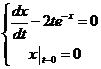 的解.求
的解.求![]() .
.
(17)(本题满分9分)求积分 ![]() .
.
(18)(本题满分11分)
求二重积分![]() 其中
其中![]()
(19)(本题满分11分)
设![]() 是区间
是区间![]() 上具有连续导数的单调增加函数,且
上具有连续导数的单调增加函数,且![]() .对任意的
.对任意的![]() ,直线
,直线![]() ,曲线
,曲线![]() 以及
以及![]() 轴所围成的曲边梯形绕
轴所围成的曲边梯形绕![]() 轴旋转一周生成一旋转体.若该旋转体的侧面积在数值上等于其体积的2倍,求函数
轴旋转一周生成一旋转体.若该旋转体的侧面积在数值上等于其体积的2倍,求函数![]() 的表达式.
的表达式.
(20)(本题满分11分)
(1) 证明积分中值定理:若函数![]() 在闭区间
在闭区间![]() 上连续,则至少存在一点
上连续,则至少存在一点![]() ,使得
,使得![]() (2)若函数
(2)若函数![]() 具有二阶导数,且满足
具有二阶导数,且满足![]() ,证明至少存在一点
,证明至少存在一点![]()
(21)(本题满分11分)
求函数![]() 在约束条件
在约束条件![]() 和
和![]() 下的最大值与最小值.
下的最大值与最小值.
(22)(本题满分12分)
![]()
设矩阵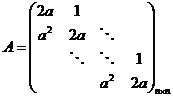 ,现矩阵
,现矩阵![]() 满足方程
满足方程![]() ,其中
,其中![]() ,
,![]() ,
,
(1)求证![]() ;
;
(2)![]() 为何值,方程组有唯一解,并求
为何值,方程组有唯一解,并求![]() ;
;
(3)![]() 为何值,方程组有无穷多解,并求通解.
为何值,方程组有无穷多解,并求通解.
(23)(本题满分10分)
设![]() 为3阶矩阵,
为3阶矩阵,![]() 为
为![]() 的分别属于特征值
的分别属于特征值![]() 特征向量,向量
特征向量,向量![]() 满足
满足![]() ,
,
(1)证明![]() 线性无关;
线性无关;
(2)令![]() ,求
,求![]() .
.
2007年全国硕士研究生入学统一考试
数学二试题
一、选择题:1~10小题,每小题4分,共40分. 在每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.
(1)当![]() 时,与
时,与![]() 等价的无穷小量是
等价的无穷小量是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]() [ ]
[ ]
(2)函数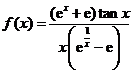 在
在![]() 上的第一类间断点是
上的第一类间断点是![]() [ ]
[ ]
(A)0 (B)1 (C)![]() (D)
(D)![]()
(3)如图,连续函数![]() 在区间
在区间![]() 上的图形分别是直径为1的上、下半圆周,在区间
上的图形分别是直径为1的上、下半圆周,在区间![]() 的图形分别是直径为2的下、上半圆周,设
的图形分别是直径为2的下、上半圆周,设![]() ,则下列结论正确的是:
,则下列结论正确的是:
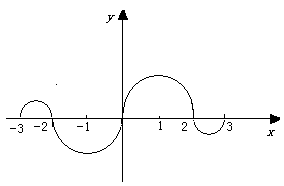
(A)![]() (B)
(B) ![]()
(C)![]() (D)
(D)![]() [ ]
[ ]
(4)设函数![]() 在
在![]() 处连续,下列命题错误的是:
处连续,下列命题错误的是:
(A)若![]() 存在,则
存在,则![]() (B)若
(B)若![]() 存在,则
存在,则![]() .
.
(C)若![]() 存在,则
存在,则![]() (D)若
(D)若![]() 存在,则
存在,则![]() .
.
[ ]
(5)曲线![]() 的渐近线的条数为
的渐近线的条数为
(A)0. (B)1. (C)2. (D)3. [ ]
(6)设函数![]() 在
在![]() 上具有二阶导数,且
上具有二阶导数,且![]() ,令
,令![]() ,则下列结论正确的是:
,则下列结论正确的是:
(A) 若![]() ,则
,则![]() 必收敛. (B) 若
必收敛. (B) 若![]() ,则
,则![]() 必发散
必发散
(C) 若![]() ,则
,则![]() 必收敛. (D) 若
必收敛. (D) 若![]() ,则
,则![]() 必发散. [ ]
必发散. [ ]
(7)二元函数![]() 在点
在点![]() 处可微的一个充要条件是[ ]
处可微的一个充要条件是[ ]
(A)![]() .
.
(B)![]() .
.
(C)![]() .
.
(D)![]() .
.
(8)设函数![]() 连续,则二次积分
连续,则二次积分![]() 等于
等于
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
(9)设向量组![]() 线性无关,则下列向量组线性相关的是
线性无关,则下列向量组线性相关的是
线性相关,则
(A) ![]() (B)
(B) ![]()
(C) ![]() . (D)
. (D) ![]() . [ ]
. [ ]
(10)设矩阵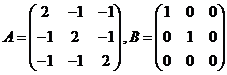 ,则
,则![]() 与
与![]()
(A) 合同且相似 (B)合同,但不相似.
(C) 不合同,但相似. (D) 既不合同也不相似 [ ]
二、填空题:11~16小题,每小题4分,共24分. 把答案填在题中横线上.
(11) ![]() __________.
__________.
(12)曲线 上对应于
上对应于![]() 的点处的法线斜率为_________.
的点处的法线斜率为_________.
(13)设函数![]() ,则
,则![]() ________.
________.
(14) 二阶常系数非齐次微分方程![]() 的通解为
的通解为![]() ________.
________.
(15) 设![]() 是二元可微函数,
是二元可微函数,![]() ,则
,则![]() __________.
__________.
(16)设矩阵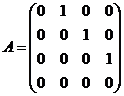 ,则
,则![]() 的秩为 .
的秩为 .
三、解答题:17~24小题,共86分. 解答应写出文字说明、证明过程或演算步骤.
(17) (本题满分10分)设![]() 是区间
是区间![]() 上单调、可导的函数,且满足
上单调、可导的函数,且满足![]() ,其中
,其中![]() 是
是![]() 的反函数,求
的反函数,求![]() .
.
(18)(本题满分11分)
设![]() 是位于曲线
是位于曲线![]() 下方、
下方、![]() 轴上方的无界区域. (Ⅰ)求区域
轴上方的无界区域. (Ⅰ)求区域![]() 绕
绕![]() 轴旋转一周所成旋转体的体积
轴旋转一周所成旋转体的体积![]() ;(Ⅱ)当
;(Ⅱ)当![]() 为何值时,
为何值时,![]() 最小?并求此最小值.
最小?并求此最小值.
(19)(本题满分10分)求微分方程![]() 满足初始条件
满足初始条件![]() 的特解.
的特解.
(20)(本题满分11分)已知函数![]() 具有二阶导数,且
具有二阶导数,且![]() ,函数
,函数![]() 由方程
由方程![]() 所确定,设
所确定,设![]() ,求
,求![]() .
.
(21) (本题满分11分)设函数![]() 在
在![]() 上连续,在
上连续,在![]() 内具有二阶导数且存在相等的最大值,
内具有二阶导数且存在相等的最大值,![]() ,证明:存在
,证明:存在![]() ,使得
,使得![]() .
.
(22) (本题满分11分) 设二元函数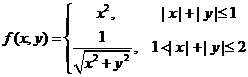 ,计算二重积分
,计算二重积分![]() ,其中
,其中![]() .
.
(23) (本题满分11分)
设线性方程组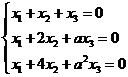 与方程
与方程![]() 有公共解,求
有公共解,求![]() 的值及所有公共解.
的值及所有公共解.
(24) (本题满分11分)
设三阶对称矩阵![]() 的特征向量值
的特征向量值![]() ,
,![]() 是
是![]() 的属于
的属于![]() 的一个特征向量,记
的一个特征向量,记![]() ,其中
,其中![]() 为3阶单位矩阵.
为3阶单位矩阵.
(I)验证![]() 是矩阵
是矩阵![]() 的特征向量,并求
的特征向量,并求![]() 的全部特征值与特征向量;
的全部特征值与特征向量;
(II)求矩阵![]() .
.
2006年全国硕士研究生入学统一考试数学二试题
填空题:1-6小题,每小题4分,共24分. 把答案填在题中横线上.
(1)曲线![]() 的水平渐近线方程为
的水平渐近线方程为
(2)设函数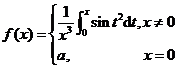 在
在![]() 处连续,则
处连续,则![]() .
.
(3)广义积分![]() .
.
(4)微分方程![]() 的通解是
的通解是
(5)设函数![]() 由方程
由方程![]() 确定,则
确定,则 ![]()
(6)设矩阵![]() ,
,![]() 为2阶单位矩阵,矩阵
为2阶单位矩阵,矩阵![]() 满足
满足![]() ,则
,则
![]() .
.
二、选择题:7-14小题,每小题4分,共32分. 每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内.
(7)设函数![]() 具有二阶导数,且
具有二阶导数,且![]() ,
,![]() 为自变量
为自变量![]() 在点
在点![]() 处的增量,
处的增量,![]() 分别为
分别为![]() 在点
在点![]() 处对应的增量与微分,若
处对应的增量与微分,若![]() ,则[ ]
,则[ ]
(A) ![]() . (B)
. (B) ![]() .
.
(C) ![]() . (D)
. (D) ![]() .
.
(8)设![]() 是奇函数,除
是奇函数,除![]() 外处处连续,
外处处连续,![]() 是其第一类间断点,则
是其第一类间断点,则![]() 是
是
(A)连续的奇函数. (B)连续的偶函数
(C)在![]() 间断的奇函数 (D)在
间断的奇函数 (D)在![]() 间断的偶函数. [ ]
间断的偶函数. [ ]
(9)设函数![]() 可微,
可微,![]() ,则
,则![]() 等于
等于
(A)![]() . (B)
. (B)![]()
(C)![]() (D)
(D)![]() [ ]
[ ]
(10)函数![]() 满足的一个微分方程是
满足的一个微分方程是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]() [ ]
[ ]
(11)设![]() 为连续函数,则
为连续函数,则![]() 等于
等于
(A)![]() . (B)
. (B)![]() .
.
(C) ![]() . (D)
. (D) ![]() . [ ]
. [ ]
(12)设![]() 均为可微函数,且
均为可微函数,且![]() ,已知
,已知![]() 是
是![]() 在约束条件
在约束条件![]() 下的一个极值点,下列选项正确的是 [ ]
下的一个极值点,下列选项正确的是 [ ]
(A) 若![]() ,则
,则![]() .
.
(B) 若![]() ,则
,则![]() .
.
(C) 若![]() ,则
,则![]() .
.
(D) 若![]() ,则
,则![]() .
.
(13)设![]() 均为
均为![]() 维列向量,
维列向量,![]() 为
为![]() 矩阵,下列选项正确的是 [ ]
矩阵,下列选项正确的是 [ ]
若![]() 线性相关,则
线性相关,则![]() 线性相关.
线性相关.
若![]() 线性相关,则
线性相关,则![]() 线性无关.
线性无关.
(C) 若![]() 线性无关,则
线性无关,则![]() 线性相关.
线性相关.
(D) 若![]() 线性无关,则
线性无关,则![]() 线性无关.
线性无关.
(14)设![]() 为3阶矩阵,将
为3阶矩阵,将![]() 的第2行加到第1行得
的第2行加到第1行得![]() ,再将
,再将![]() 的第1列的
的第1列的![]() 倍加到第2列得
倍加到第2列得![]() ,记
,记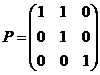 ,则
,则
(A)![]() . (B)
. (B)![]() .
.
(C)![]() . (D)
. (D)![]() . [ ]
. [ ]
三 、解答题:15-23小题,共94分.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分10分)
试确定![]() 的值,使得
的值,使得![]() ,其中
,其中![]() 是当
是当![]() 时比
时比![]() 高阶的无穷小.
高阶的无穷小.
(16)(本题满分10分)求 ![]() .
.
(17)(本题满分10分)设区域![]() , 计算二重积分
, 计算二重积分![]()
(18)(本题满分12分)设数列![]() 满足
满足![]()
(Ⅰ)证明![]() 存在,并求该极限;(Ⅱ)计算
存在,并求该极限;(Ⅱ)计算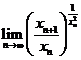 .
.
(19)(本题满分10分)
证明:当![]() 时,
时,
![]() .
.
(20)(本题满分12分)
设函数![]() 在
在![]() 内具有二阶导数,且
内具有二阶导数,且![]() 满足等式
满足等式![]() .
.
(I)验证![]() ;
;
(II)若![]() ,求函数
,求函数![]() 的表达式.
的表达式.
(21)(本题满分12分)
已知曲线L的方程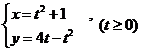 (I)讨论L的凹凸性;(II)过点
(I)讨论L的凹凸性;(II)过点![]() 引L的切线,求切点
引L的切线,求切点![]() ,并写出切线的方程;(III)求此切线与L(对应于
,并写出切线的方程;(III)求此切线与L(对应于![]() 的部分)及x轴所围成的平面图形的面积.
的部分)及x轴所围成的平面图形的面积.
(22)(本题满分9分)
已知非齐次线性方程组
 有3个线性无关的解.(Ⅰ)证明方程组系数矩阵
有3个线性无关的解.(Ⅰ)证明方程组系数矩阵![]() 的秩
的秩![]() ;(Ⅱ)求
;(Ⅱ)求![]() 的值及方程组的通解.
的值及方程组的通解.
(23)(本题满分9分)
设3阶实对称矩阵![]() 的各行元素之和均为3,向量
的各行元素之和均为3,向量![]() 是线性方程组
是线性方程组![]() 的两个解.
的两个解.
(Ⅰ) 求![]() 的特征值与特征向量;
的特征值与特征向量;
(Ⅱ) 求正交矩阵![]() 和对角矩阵
和对角矩阵![]() ,使得
,使得![]() .
.
2005年全国硕士研究生入学统一考试
数学二试题
填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上)
(1)设![]() ,则
,则![]() = .
= .
(2)曲线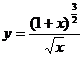 的斜渐近线方程为 .
的斜渐近线方程为 .
(3)![]() .
.
(4)微分方程![]() 满足
满足![]() 的解为 .
的解为 .
(5)当![]() 时,
时,![]() 与
与![]() 是等价无穷小,则k= .
是等价无穷小,则k= .
(6)设![]() 均为3维列向量,记矩阵
均为3维列向量,记矩阵
![]() ,
,![]() ,
,
如果![]() ,那么
,那么![]() .
.
二、选择题(本题共8小题,每小题4分,满分32分. 每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)
(7)设函数![]() ,则f(x)在
,则f(x)在![]() 内
内
(A) 处处可导. (B) 恰有一个不可导点.
(C) 恰有两个不可导点. (D) 至少有三个不可导点. [ ]
(8)设F(x)是连续函数f(x)的一个原函数,![]() 表示“M的充分必要条件是N”,则必有
表示“M的充分必要条件是N”,则必有
F(x)是偶函数![]() f(x)是奇函数.
f(x)是奇函数.
(B) F(x)是奇函数![]() f(x)是偶函数.
f(x)是偶函数.
(C) F(x)是周期函数![]() f(x)是周期函数.
f(x)是周期函数.
(D) F(x)是单调函数![]() f(x)是单调函数. [ ]
f(x)是单调函数. [ ]
(9)设函数y=y(x)由参数方程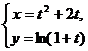 确定,则曲线y=y(x)在x=3处的法线与x轴交点的横坐标是
确定,则曲线y=y(x)在x=3处的法线与x轴交点的横坐标是
(A) ![]() . (B)
. (B) ![]() .
.
(C) ![]() . (D)
. (D) ![]() . [ ]
. [ ]
(10)设区域![]() ,f(x)为D上的正值连续函数,a,b为常数,则
,f(x)为D上的正值连续函数,a,b为常数,则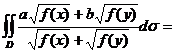
(A) ![]() . (B)
. (B) ![]() . (C)
. (C) ![]() . (D)
. (D) ![]() . [ ]
. [ ]
(11)设函数![]() , 其中函数
, 其中函数![]() 具有二阶导数,
具有二阶导数,![]() 具有一阶导数,则必有
具有一阶导数,则必有
(A) ![]() . (B)
. (B) ![]() .
.
(C) ![]() . (D)
. (D) ![]() . [ ]
. [ ]
(12)设函数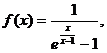 则
则
x=0,x=1都是f(x)的第一类间断点.
(B) x=0,x=1都是f(x)的第二类间断点.
(C) x=0是f(x)的第一类间断点,x=1是f(x)的第二类间断点.
x=0是f(x)的第二类间断点,x=1是f(x)的第一类间断点. [ ]
(13)设![]() 是矩阵A的两个不同的特征值,对应的特征向量分别为
是矩阵A的两个不同的特征值,对应的特征向量分别为![]() ,则
,则![]() ,
,![]() 线性无关的充分必要条件是
线性无关的充分必要条件是
(A) ![]() . (B)
. (B) ![]() . (C)
. (C) ![]() . (D)
. (D) ![]() . [ ]
. [ ]
(14)设A为n(![]() )阶可逆矩阵,交换A的第1行与第2行得矩阵B,
)阶可逆矩阵,交换A的第1行与第2行得矩阵B, ![]() 分别为A,B的伴随矩阵,则 [ ]
分别为A,B的伴随矩阵,则 [ ]
交换![]() 的第1列与第2列得
的第1列与第2列得![]() . (B) 交换
. (B) 交换![]() 的第1行与第2行得
的第1行与第2行得![]() .
.
(C) 交换![]() 的第1列与第2列得
的第1列与第2列得![]() . (D) 交换
. (D) 交换![]() 的第1行与第2行得
的第1行与第2行得![]() . 三 、解答题(本题共9小题,满分94分.解答应写出文字说明、证明过程或演算步骤.)
. 三 、解答题(本题共9小题,满分94分.解答应写出文字说明、证明过程或演算步骤.)
(15)(本题满分11分)设函数f(x)连续,且![]() ,求极限
,求极限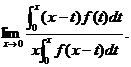

(16)(本题满分11分)
如图,![]() 和
和![]() 分别是
分别是![]() 和
和![]() 的图象,过点(0,1)的曲线
的图象,过点(0,1)的曲线![]() 是一单调增函数的图象. 过
是一单调增函数的图象. 过![]() 上任一点M(x,y)分别作垂直于x轴和y轴的直线
上任一点M(x,y)分别作垂直于x轴和y轴的直线![]() 和
和![]() . 记
. 记![]() 与
与![]() 所围图形的面积为
所围图形的面积为![]() ;
;![]() 与
与![]() 所围图形的面积为
所围图形的面积为![]() 如果总有
如果总有![]() ,求曲线
,求曲线![]() 的方程
的方程![]()

(17)(本题满分11分)
如图,曲线C的方程为y=f(x),点(3,2)是它的一个拐点,直线![]() 与
与![]() 分别是曲线C在点(0,0)与(3,2)处的切线,其交点为(2,4). 设函数f(x)具有三阶连续导数,计算定积分
分别是曲线C在点(0,0)与(3,2)处的切线,其交点为(2,4). 设函数f(x)具有三阶连续导数,计算定积分![]()
(18)(本题满分12分)
用变量代换![]() 化简微分方程
化简微分方程![]() ,并求其满足
,并求其满足![]() 的特解.
的特解.
(19)(本题满分12分)已知函数f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,f(1)=1. 证明:
(I)存在![]() 使得
使得![]() ;(II)存在两个不同的点
;(II)存在两个不同的点![]() ,使得
,使得![]()
(20)(本题满分10分)
已知函数z=f(x,y) 的全微分![]() ,并且f(1,1,)=2. 求f(x,y)在椭圆域
,并且f(1,1,)=2. 求f(x,y)在椭圆域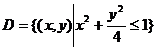 上的最大值和最小值.
上的最大值和最小值.
(21)(本题满分9分)
计算二重积分![]() ,其中
,其中![]() .
.
(22)(本题满分9分)
确定常数a,使向量组![]()
![]()
![]() 可由向量组
可由向量组![]()
![]()
![]() 线性表示,但向量组
线性表示,但向量组![]() 不能由向量组
不能由向量组![]() 线性表示.
线性表示.
(23)(本题满分9分)
已知3阶矩阵A的第一行是![]() 不全为零,矩阵
不全为零,矩阵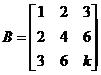 (k为常数),且AB=O, 求线性方程组Ax=0的通解.
(k为常数),且AB=O, 求线性方程组Ax=0的通解.
2004年考硕数学(二)真题
一. 填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上. )
(1)设![]() , 则
, 则![]() 的间断点为
的间断点为![]() .
.
(2)设函数![]() 由参数方程
由参数方程 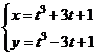 确定, 则曲线
确定, 则曲线![]() 向上凸的
向上凸的![]() 取值范围为____..
取值范围为____..
(3)![]() _____..
_____..
(4)设函数![]() 由方程
由方程![]() 确定, 则
确定, 则![]() ______.
______.
(5)微分方程![]() 满足
满足![]() 的特解为_______.
的特解为_______.
(6)设矩阵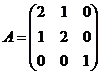 , 矩阵
, 矩阵![]() 满足
满足![]() , 其中
, 其中![]() 为
为![]() 的伴随矩阵,
的伴随矩阵, ![]() 是单位矩阵, 则
是单位矩阵, 则![]() ______-.
______-.
二. 选择题(本题共8小题,每小题4分,满分32分. 每小题给出的四个选项中,只有一项符合题目要求, 把所选项前的字母填在题后的括号内. )
(7)把![]() 时的无穷小量
时的无穷小量![]() ,
, ![]() ,
, ![]() 排列起来, 使排在后面的是前一个的高阶无穷小, 则正确的排列次序是
排列起来, 使排在后面的是前一个的高阶无穷小, 则正确的排列次序是
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
![]()
(8)设![]() , 则
, 则
(A)![]() 是
是![]() 的极值点, 但
的极值点, 但![]() 不是曲线
不是曲线![]() 的拐点.
的拐点.
(B)![]() 不是
不是![]() 的极值点, 但
的极值点, 但![]() 是曲线
是曲线![]() 的拐点.
的拐点.
(C)![]() 是
是![]() 的极值点, 且
的极值点, 且![]() 是曲线
是曲线![]() 的拐点.
的拐点.
(D)![]() 不是
不是![]() 的极值点,
的极值点, ![]() 也不是曲线
也不是曲线![]() 的拐点.
的拐点. ![]()
(9)![]() 等于
等于
(A)![]() . (B)
. (B)![]() .
.
(C)![]() . (D)
. (D)![]()
![]()
(10)设函数![]() 连续, 且
连续, 且![]() , 则存在
, 则存在![]() , 使得
, 使得
(A)![]() 在
在![]() 内单调增加.
内单调增加.
(B)![]() 在
在![]() 内单调减小.
内单调减小.
(C)对任意的![]() 有
有![]() .
.
(D)对任意的![]() 有
有![]() .
. ![]()
(11)微分方程![]() 的特解形式可设为
的特解形式可设为
(A)![]() .
.
(B)![]() .
.
(C)![]() .
.
(D)![]()
![]()
(12)设函数![]() 连续, 区域
连续, 区域![]() , 则
, 则![]() 等于
等于
(A)![]() .
.
(B)![]() .
.
(C)![]() .
.
(D)![]()
![]()
(13)设![]() 是3阶方阵, 将
是3阶方阵, 将![]() 的第1列与第2列交换得
的第1列与第2列交换得![]() , 再把
, 再把![]() 的第2列加到第3列得
的第2列加到第3列得![]() , 则满足
, 则满足![]() 的可逆矩阵
的可逆矩阵![]() 为
为
(A)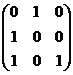 . (B)
. (B)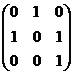 .
.
(C)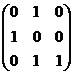 . (D)
. (D)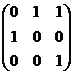 .
. ![]()
(14)设![]() ,
,![]() 为满足
为满足![]() 的任意两个非零矩阵, 则必有
的任意两个非零矩阵, 则必有
(A)![]() 的列向量组线性相关,
的列向量组线性相关,![]() 的行向量组线性相关.
的行向量组线性相关.
(B)![]() 的列向量组线性相关,
的列向量组线性相关,![]() 的列向量组线性相关.
的列向量组线性相关.
(C)![]() 的行向量组线性相关,
的行向量组线性相关,![]() 的行向量组线性相关.
的行向量组线性相关.
(D)![]() 的行向量组线性相关,
的行向量组线性相关,![]() 的列向量组线性相关.
的列向量组线性相关. ![]()
三. 解答题(本题共9小题,满分94分. 解答应写出文字说明、证明过程或演算步骤. )
(15)(本题满分10分)
求极限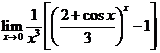 .
.
(16)(本题满分10分)
设函数![]() 在(
在(![]() )上有定义, 在区间
)上有定义, 在区间![]() 上,
上, ![]() , 若对任意的
, 若对任意的![]() 都满足
都满足![]() , 其中
, 其中![]() 为常数.
为常数.
(Ⅰ)写出![]() 在
在![]() 上的表达式; (Ⅱ)问
上的表达式; (Ⅱ)问![]() 为何值时,
为何值时, ![]() 在
在![]() 处可导.
处可导.
(17)(本题满分11分)
设![]() ,(Ⅰ)证明
,(Ⅰ)证明![]() 是以
是以![]() 为周期的周期函数;(Ⅱ)求
为周期的周期函数;(Ⅱ)求![]() 的值域.
的值域.
(18)(本题满分12分)
曲线![]() 与直线
与直线![]() 及
及![]() 围成一曲边梯形. 该曲边梯形绕
围成一曲边梯形. 该曲边梯形绕![]() 轴旋转一周得一旋转体, 其体积为
轴旋转一周得一旋转体, 其体积为![]() , 侧面积为
, 侧面积为![]() , 在
, 在![]() 处的底面积为
处的底面积为![]() .
.
(Ⅰ)求![]() 的值; (Ⅱ)计算极限
的值; (Ⅱ)计算极限![]() .
.
(19)(本题满分12分)设![]() , 证明
, 证明![]() .
.
(20)(本题满分11分)
某种飞机在机场降落时,为了减小滑行距离,在触地的瞬间,飞机尾部张开减速伞,以增大阻力,使飞机迅速减速并停下来.现有一质量为![]() 的飞机,着陆时的水平速度为
的飞机,着陆时的水平速度为![]() .经测试,减速伞打开后,飞机所受的总阻力与飞机的速度成正比(比例系数为
.经测试,减速伞打开后,飞机所受的总阻力与飞机的速度成正比(比例系数为![]() ).问从着陆点算起,飞机滑行的最长距离是多少?
).问从着陆点算起,飞机滑行的最长距离是多少?
注 ![]() 表示千克,
表示千克,![]() 表示千米/小时.
表示千米/小时.
(21)(本题满分10分)设![]() ,其中
,其中![]() 具有连续二阶偏导数,求
具有连续二阶偏导数,求![]() .
.
(22)(本题满分9分)
设有齐次线性方程组
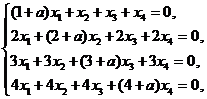
试问![]() 取何值时, 该方程组有非零解, 并求出其通解.
取何值时, 该方程组有非零解, 并求出其通解.
(23)(本题满分9分)
设矩阵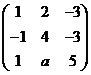 的特征方程有一个二重根, 求
的特征方程有一个二重根, 求![]() 的值, 并讨论
的值, 并讨论![]() 是否可相似对角化.
是否可相似对角化.
2003年考研数学(二)真题
填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上)
(1) 若![]() 时,
时,![]() 与
与![]() 是等价无穷小,则a= .
是等价无穷小,则a= .
(2) 设函数y=f(x)由方程![]() 所确定,则曲线y=f(x)在点(1,1)处的切线方程是 .
所确定,则曲线y=f(x)在点(1,1)处的切线方程是 .
(3) ![]() 的麦克劳林公式中
的麦克劳林公式中![]() 项的系数是__________.
项的系数是__________.
(4) 设曲线的极坐标方程为![]() ,则该曲线上相应于
,则该曲线上相应于![]() 从0变到
从0变到![]() 的一段弧与极轴所围成的图形的面积为__________.
的一段弧与极轴所围成的图形的面积为__________.
(5) 设![]() 为3维列向量,
为3维列向量,![]() 是
是![]() 的转置. 若
的转置. 若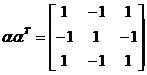 ,则
,则
![]() = .
= .
(6) 设三阶方阵A,B满足![]() ,其中E为三阶单位矩阵,若
,其中E为三阶单位矩阵,若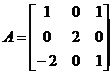 ,则
,则![]() ________.
________.
二、选择题(本题共6小题,每小题4分,满分24分. 每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)
(1)设![]() 均为非负数列,且
均为非负数列,且![]() ,
,![]() ,
,![]() ,则必有
,则必有
(A) ![]() 对任意n成立. (B)
对任意n成立. (B) ![]() 对任意n成立.
对任意n成立.
(C) 极限![]() 不存在. (D) 极限
不存在. (D) 极限![]() 不存在. [ ]
不存在. [ ]
(2)设![]() , 则极限
, 则极限![]() 等于
等于
(A) ![]() . (B)
. (B) ![]() .
.
(C) ![]() . (D)
. (D) ![]() . [ ]
. [ ]
(3)已知![]() 是微分方程
是微分方程![]() 的解,则
的解,则![]() 的表达式为
的表达式为
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]() [ ]
[ ]
(4)设函数f(x)在![]() 内连续,其导函数的图形如图所示,则f(x)有
内连续,其导函数的图形如图所示,则f(x)有
一个极小值点和两个极大值点.
两个极小值点和一个极大值点.
两个极小值点和两个极大值点.
(D) 三个极小值点和一个极大值点. [ ]
y
O x
(5)设![]() ,
,![]() , 则
, 则
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]() [ ]
[ ]
(6)设向量组I:![]() 可由向量组II:
可由向量组II:![]() 线性表示,则
线性表示,则
(A) 当![]() 时,向量组II必线性相关. (B) 当
时,向量组II必线性相关. (B) 当![]() 时,向量组II必线性相关.
时,向量组II必线性相关.
(C) 当![]() 时,向量组I必线性相关. (D) 当
时,向量组I必线性相关. (D) 当![]() 时,向量组I必线性相关.
时,向量组I必线性相关.
[ ]
三 、(本题满分10分)设函数 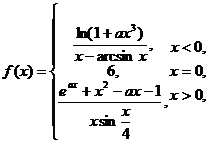
问a为何值时,f(x)在x=0处连续;a为何值时,x=0是f(x)的可去间断点?
四 、(本题满分9分)
设函数y=y(x)由参数方程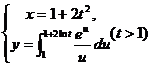 所确定,求
所确定,求![]()
五 、(本题满分9分)计算不定积分 
六 、(本题满分12分)
设函数y=y(x)在![]() 内具有二阶导数,且
内具有二阶导数,且![]() 是y=y(x)的反函数.
是y=y(x)的反函数.
(1) 试将x=x(y)所满足的微分方程![]() 变换为y=y(x)满足的微分方程;
变换为y=y(x)满足的微分方程;
(2) 求变换后的微分方程满足初始条件![]() 的解.
的解.
七 、(本题满分12分)
讨论曲线![]() 与
与![]() 的交点个数.
的交点个数.
八 、(本题满分12分)
设位于第一象限的曲线y=f(x)过点![]() ,其上任一点P(x,y)处的法线与y轴的交点为Q,且线段PQ被x轴平分.
,其上任一点P(x,y)处的法线与y轴的交点为Q,且线段PQ被x轴平分.
求曲线 y=f(x)的方程;
已知曲线y=sinx在![]() 上的弧长为
上的弧长为![]() ,试用
,试用![]() 表示曲线y=f(x)的弧长s.
表示曲线y=f(x)的弧长s.
九 、(本题满分10分)
有一平底容器,其内侧壁是由曲线![]() 绕y轴旋转而成的旋转曲面(如图),容器的底面圆的半径为2 m.根据设计要求,当以
绕y轴旋转而成的旋转曲面(如图),容器的底面圆的半径为2 m.根据设计要求,当以![]() 的速率向容器内注入液体时,液面的面积将以
的速率向容器内注入液体时,液面的面积将以![]() 的速率均匀扩大(假设注入液体前,容器内无液体).
的速率均匀扩大(假设注入液体前,容器内无液体).
根据t时刻液面的面积,写出t与![]() 之间的关系式;
之间的关系式;
求曲线![]() 的方程.
的方程.
(注:m表示长度单位米,min表示时间单位分.)
十 、(本题满分10分)设函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且![]() 若极限
若极限![]() 存在,证明:
存在,证明:
在(a,b)内f(x)>0; (2)在(a,b)内存在点![]() ,使
,使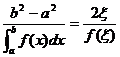 ;
;
(3) 在(a,b) 内存在与(2)中![]() 相异的点
相异的点![]() ,使
,使![]()
十 一、(本题满分10分)
若矩阵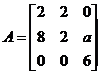 相似于对角阵
相似于对角阵![]() ,试确定常数a的值;并求可逆矩阵P使
,试确定常数a的值;并求可逆矩阵P使![]()
十二 、(本题满分8分)
已知平面上三条不同直线的方程分别为
![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() .
.
试证这三条直线交于一点的充分必要条件为![]()
2016考研数学(一)真题完整版
一、选择题:1~8小题,每小题4分,共32分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答题纸指定位置上.
(1)若反常积分![]() 收敛,则( )
收敛,则( )
![]()
(2)已知函数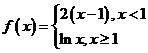 ,则
,则![]() 的一个原函数是( )
的一个原函数是( )
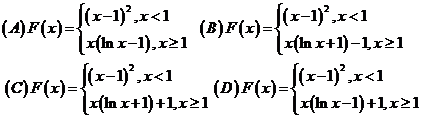
(3)若![]() 是微分方程
是微分方程![]() 的两个解,则
的两个解,则![]() ( )
( )
![]()
(4)已知函数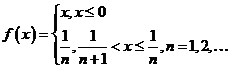 ,则( )
,则( )
(A)![]() 是
是![]() 的第一类间断点 (B)
的第一类间断点 (B)![]() 是
是![]() 的第二类间断点
的第二类间断点
(C)![]() 在
在![]() 处连续但不可导 (D)
处连续但不可导 (D)![]() 在
在![]() 处可导
处可导
(5)设A,B是可逆矩阵,且A与B相似,则下列结论错误的是( )
(A)![]() 与
与![]() 相似 (B)
相似 (B)![]() 与
与![]() 相似
相似
(C)![]() 与
与![]() 相似 (D)
相似 (D)![]() 与
与![]() 相似
相似
(6)设二次型![]() ,则
,则![]() 在空间直角坐标下表示的二次曲面为( )
在空间直角坐标下表示的二次曲面为( )
(A)单叶双曲面 (B)双叶双曲面 (C)椭球面 (C)柱面
(7)设随机变量![]() ,记
,记![]() ,则( )
,则( )
(A)![]() 随着
随着![]() 的增加而增加 (B)
的增加而增加 (B)![]() 随着
随着![]() 的增加而增加
的增加而增加
(C)![]() 随着
随着![]() 的增加而减少 (D)
的增加而减少 (D)![]() 随着
随着![]() 的增加而减少
的增加而减少
(8)随机试验![]() 有三种两两不相容的结果
有三种两两不相容的结果![]() ,且三种结果发生的概率均为
,且三种结果发生的概率均为![]() ,将试验
,将试验![]() 独立重复做2次,
独立重复做2次,![]() 表示2次试验中结果
表示2次试验中结果![]() 发生的次数,
发生的次数,![]() 表示2次试验中结果
表示2次试验中结果![]() 发生的次数,则
发生的次数,则![]() 与
与![]() 的相关系数为( )
的相关系数为( )
二、填空题:9-14小题,每小题4分,共24分,请将答案写在答题纸指定位置上.
(9)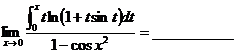
(10)向量场![]() 的旋度
的旋度![]()
(11)设函数![]() 可微,
可微,![]() 由方程
由方程![]() 确定,则
确定,则![]()
(12)设函数![]() ,且
,且![]() ,则
,则![]()
(13)行列式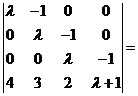 ____________.
____________.
(14)设![]() 为来自总体
为来自总体![]() 的简单随机样本,样本均值
的简单随机样本,样本均值![]() ,参数
,参数![]() 的置信度为0.95的双侧置信区间的置信上限为10.8,则
的置信度为0.95的双侧置信区间的置信上限为10.8,则![]() 的置信度为0.95的双侧置信区间为______.
的置信度为0.95的双侧置信区间为______.
三、解答题:15—23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.
(15)(本题满分10分)已知平面区域![]() ,计算二重积分
,计算二重积分![]() .
.
(16)(本题满分10分)设函数![]() 满足方程
满足方程![]() 其中
其中![]() .
.
![]() 证明:反常积分
证明:反常积分![]() 收敛;
收敛;
![]() 若
若![]() 求
求![]() 的值.
的值.
(17)(本题满分10分)设函数![]() 满足
满足![]() 且
且![]() 是从点
是从点![]() 到点
到点![]() 的光滑曲线,计算曲线积分
的光滑曲线,计算曲线积分![]() ,并求
,并求![]() 的最小值
的最小值
(18)设有界区域![]() 由平面
由平面![]() 与三个坐标平面围成,
与三个坐标平面围成,![]() 为
为![]() 整个表面的外侧,计算曲面积分
整个表面的外侧,计算曲面积分![]()
(19)(本题满分10分)已知函数![]() 可导,且
可导,且![]() ,
,![]() ,设数列
,设数列![]() 满足
满足![]() ,证明:
,证明:
(I)级数![]() 绝对收敛;
绝对收敛;
(II)![]() 存在,且
存在,且![]() .
.
(20)(本题满分11分)设矩阵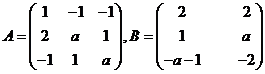
当![]() 为何值时,方程
为何值时,方程![]() 无解、有唯一解、有无穷多解?
无解、有唯一解、有无穷多解?
(21)(本题满分11分)已知矩阵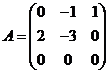
(I)求![]()
(II)设3阶矩阵![]() 满足
满足![]() ,记
,记![]() 将
将![]() 分别表示为
分别表示为![]() 的线性组合。
的线性组合。
(22)(本题满分11分)设二维随机变量![]() 在区域
在区域![]() 上服从均匀分布,令
上服从均匀分布,令
![]()
(I)写出![]() 的概率密度;
的概率密度;
(II)问![]() 与
与![]() 是否相互独立?并说明理由;
是否相互独立?并说明理由;
(III)求![]() 的分布函数
的分布函数![]() .
.
(23)设总体![]() 的概率密度为
的概率密度为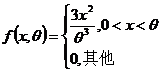 ,其中
,其中![]() 为未知参数,
为未知参数,![]() 为来自总体
为来自总体![]() 的简单随机样本,令
的简单随机样本,令![]() 。
。
(1)求![]() 的概率密度
的概率密度
(2)确定![]() ,使得
,使得![]() 为
为![]() 的无偏估计
的无偏估计



15
5) 设函数![]() 满足
满足![]() ,则
,则![]() 与
与![]() 依次是 ( )
依次是 ( )
(A) (B) (C) (D)
【答案】(D)
【解析】此题考查二元复合函数偏导的求解.
令,则,从而变为
.故,
因而.故选(D).
(6)设是第一象限由曲线,与直线,围成的平面区域,函数在上连续,则 ( )
(A)
(B)
(C)
(D)
【答案】(B)
【解析】根据图可得,在极坐标系下计算该二重积分的积分区域为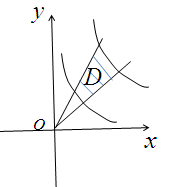
所以
故选B.